MIX10: A MATLAB TO X10 COMPILER FOR HIGH PERFORMANCE
by
Vineet Kumar
School of Computer Science
McGill University, Montréal
Monday, April 14th 2014
A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES AND RESEARCH
IN PARTIAL FULfiLLMENT OF THE REQUIREMENTS FOR THE DEGREE OF
MASTER OF SCIENCE
Copyright
© 2014 Vineet Kumar
Abstract
MATLAB is a popular dynamic array-based language commonly used by students, scientists
and engineers who appreciate the interactive development style, the rich set of array operators, the
extensive builtin library, and the fact that they do not have to declare static types. Even though
these users like to program in MATLAB, their computations are often very compute-intensive
and are better suited for emerging high performance computing systems. This thesis
reports on MIX10, a source-to-source compiler that automatically translates MATLAB
programs to X10, a language designed for “Performance and Productivity at Scale";
thus, helping scientific programmers make better use of high performance computing
systems.
There is a large semantic gap between the array-based dynamically-typed nature of MATLAB
and the object-oriented, statically-typed, and high-level array abstractions of X10. This thesis
addresses the major challenges that must be overcome to produce sequential X10 code that is
competitive with state-of-the-art static compilers for MATLAB which target more conventional
imperative languages such as C and Fortran. Given that efficient basis, the thesis then provides a
translation for the MATLAB parfor construct that leverages the powerful concurrency
constructs in X10.
The MIX10 compiler has been implemented using the McLab compiler tools, is
open source, and is available both for compiler researchers and end-user MATLAB
programmers. We have used the implementation to perform many empirical measurements on
a set of 17 MATLAB benchmarks. We show that our best MIX10-generated code is
significantly faster than the de facto Mathworks’ MATLAB system, and that our results are
competitive with state-of-the-art static compilers that target C and Fortran. We also show
the importance of finding the correct approach to representing the arrays in X10, and
the necessity of an IntegerOkay analysis that determines which double variables can
be safely represented as integers. Finally, we show that our X10-based handling of
the MATLAB parfor greatly outperforms the de facto MATLAB implementation.
Résumé
MATLAB est un langage de programmation dynamique, orienté-tableaux communément
utilisé par les étudiants, les scientifiques et les ingénieurs qui apprécient son style de
développement interactif, la richesse de ses opérateurs sur les tableaux, sa librairie
impressionnante de fonctions de base et le fait qu’on aie pas à déclarer statiquement le type des
variables. Bien que ces usagers apprécient MATLAB, leurs programmes nécessitent souvent des
ressources de calcul importantes qui sont offertes par les nouveaux systèmes de haute
performance. Cette thèse fait le rapport de MIX10, un compilateur source-à-source qui fait la
traduction automatique de programmes MATLAB à X10, un langage construit pour "la
performance et la productivité à grande échelle." Ainsi, MIX10 aide les programmeurs
scientifiques à faire un meilleur usage des ressources des systèmes de calcul de haute
performance.
Il y a un écart sémantique important entre le typage dynamique et le focus sur les tableaux de
MATLAB et l’approche orientée-objet, le typage statique et les abstractions de haut niveau sur les
tableaux de X10. Cette thèse discute des défis principaux qui doivent être surmontés afin de
produire du code X10 séquentiel compétitif avec les meilleurs compilateurs statiques pour
MATLAB qui traduisent vers des langages impératifs plus conventionnels, tels que C et Fortran.
Fort de cette fondation efficace, cette thèse décrit ensuite la traduction de l’instruction parfor
de MATLAB afin d’utiliser les opérations sophistiquées de traitement concurrent de
X10.
Le compilateur MIX10 a été implémenté à l’aide de la suite d’outils de McLab, un projet
libre de droits, disponible à la communauté de recherche ainsi qu’aux utilisateurs de MATLAB.
Nous avons utilisé notre implémentation afin d’effectuer des mesures empiriques de performance
sur un jeu de 17 programmes MATLAB. Nous démontrons que le code généré par MIX10 est
considérablement plus rapide que le système MATLAB de Mathworks et que nos résultats sont
compétitifs avec les meilleurs compilateurs statiques qui produisent du code C et Fortran.
Nous montrons également l’importance d’une représentation appropriée des tableaux
en X10 et la nécessité d’une analyse IntegerOkay qui permet de déterminer quelles
variables de type réel (double) peuvent être correctement représentées par des entiers (int).
Finalement, nous montrons que notre traitement de l’instruction parfor en X10 nous
permet d’atteindre des vitesses d’exécution considérablement meilleures que dans
MATLAB.
Acknowledgements
I am thankful to my supervisor, Laurie Hendren, whose constant encouragement and guidance
not only helped me to understand compilers better, but also helped me become a better writer and
a better presenter.
I would like to give a special thanks to David Grove for suggesting this line of research and in
helping us understand key parts of the X10 language and implementation.
I am also thankful to the McLAB team for building an amazing framework for compiler
research on MATLAB. In particular, I am thankful to Anton Dubrau (M.Sc.) for helping me
understand the MCSAF and Tamer frameworks, and Xu Li (M.Sc.) for all the interesting
discussions on how to statically compile MATLAB.
Finally, I would like to thank my parents and my brother, who made it possible for me to
pursue my M.Sc. degree.
Apart from all the wonderful people around me, I am thankful to my computers, Antriksh,
Heisenberg, and cougar.cs.mcgill.ca for tirelessly and reliably crunching numbers day in and day
out.
This work was supported, in part, by the Natural Sciences and Engineering Research Council
of Canada (NSERC).
Table of Contents
List of Figures
List of Tables
Chapter 1
Introduction
___________________________________________________________________________________
MATLAB is a popular numeric programming language, used by millions of scientists,
engineers as well as students worldwide[Mol]. MATLAB programmers appreciate the high-level
matrix operators, the fact that variables and types do not need to be declared, the large number of
library and builtin functions available, and the interactive style of program development available
through the IDE and the interpreter-style read-eval-print loop. However, even though MATLAB
programmers appreciate all of the features that enable rapid prototyping, their applications are
often quite compute intensive and time consuming. These applications could perform
much more efficiently if they could be easily ported to a high performance computing
system.
X10 [IBM12], on the other hand, is an object-oriented and statically-typed language which
uses cilk-style arrays indexed by Point objects and rail-backed multidimensional arrays, and has
been designed with well-defined semantics and high performance computing in mind. The X10
compiler can generate C++ or Java code and supports various communication interfaces
including sockets and MPI for communication between nodes on a parallel computing
system.
In this thesis we present MIX10, a source-to-source compiler that helps to bridge the gap
between MATLAB, a language familiar to scientists, and X10, a language designed for high
performance computing systems. MIX10 statically compiles MATLAB programs to X10 and thus
allows scientists and engineers to write programs in MATLAB (or use old programs already
written in MATLAB) and still get the benefits of high performance computing without having to
learn a new language.Also, systems that use MATLAB for prototyping and C++ or Java for
production, can benefit from MIX10 by quickly convert- ing MATLAB prototypes to C++ or Java
programs via X10
On one hand, all the aforementioned characteristics of MATLAB make it a very user-friendly
and thus a popular application to develop software among a non-programmer community.
On the other hand, these same characteristics make MATLAB a difficult language to
compile statically. Even the de facto standard, Mathworks’ implementation of MATLAB is
essentially an interpreter with a JIT accelarator[The02] which is generally slower than
statically compiled languages. GNU Octave, which is a popular open source alternative to
MATLAB and is mostly compatible with MATLAB, introduced JIT compilation only in
its most recent release 3.8 in March 2014. Before that it was implemented only as an
interpreter[Oct]. Lack of formal language specification, unconventional semantics and closed
source make it even harder to write a compiler for MATLAB. These are some of the
challenges that MIX10 shares with other static compilers which convert MATLAB
to C or Fortran. However, targeting X10 raises some significant new challenges. For
example, X10 is an object-oriented, heap-based, language with varying levels of high-level
abstractions for arrays and iterators of arrays. An open question was whether or not it was
possible to generate X10 code that both maintains the MATLAB semantics, but also
leads to code that is as efficient as state-of-the-art translators that target C and Fortran.
Finding an effective and efficient translation from MATLAB to X10 was not obvious,
and this thesis reports on the key problems we encountered and the solutions that we
designed and implemented in our MIX10 system. By demonstrating that we can generate
sequential X10 code that is as efficient as generated C or Fortran code, we then enabled the
possibility of leveraging the high performance nature of X10’s parallel constructs. To
demonstrate this, we exposed scalable concurrency in MATLAB via X10 and examined
how to use X10 features to provide a good implementation for MATLAB’s parfor
construct.
Built on top of McLAB static analysis framework[Doh11, DH12b], MIX10, together with its
set of reusable static analyses for performance optimization and extended support for MATLAB
features, ultimately aims to provide MATLAB’s ease of use, sequential performance comparable to
that provided by state-of-the art compilers targetting C and Fortran, to support parallel constructs
like parfor and to expose scalable concurrency.
1.1 Contributions
The major contributions of this thesis are as follows:
-
Identifying key challenges:
- We have identified the key challenges in performing a
semantics-preserving efficient translation of MATLAB to X10.
-
Overall design of MIX10:
- Building upon the McLAB frontend and analysis framework,
we provide the design of the MIX10 source-to-source translator that includes a
low-level X10 IR and a template-based specialization framework for handling builtin
operations.
-
Techniques for efficient compilation of MATLAB arrays:
-
Arrays are the core of MATLAB. All data, including scalar values are represented as
arrays in MATLAB. Efficient compilation of arrays is the key for good performance.
X10 provides two types of array representations for multidimensional arrays: (1)
Cilk-styled, region-based arrays and (2) rail-backed simple arrays. We compare and
contrast these two array forms for a high performance computing language in context
of being used as a target language and provide techniques to compile MATLAB arrays
to two different representations of arrays provided by X10.
-
Builtin handling framework:
- We have designed and implemented a template-based
system that allows us to generate specialized X10 code for a collection of important
MATLAB builtin operations.
-
Code generation strategies for the sequential core:
- There are some very significant
differences between the semantics of MATLAB and X10. A key difference is that
MATLAB is dynamically-typed, whereas X10 is statically-typed. Furthermore, the
type rules are quite different, which means that the generated X10 code must include
the appropriate explicit type conversion rules, so as to match the MATLAB semantics.
Other MATLAB features, such as multiple returns from functions, a non-standard
semantics for for loops, and a very general range operator, must also be handled
correctly.
-
Code generation for concurrency in MATLAB:
- MIX10 not only supports all the key
sequential constructs but also supports concurrency constructs like parfor and
can handle vectorized instructions in a concurrent fashion. We have also introduced
X10-like concurrency constructs in MATLAB via structured comments.
-
Safe use of integer variables:
- Even after determining the correct use of X10 arrays, we
were still faced with a performance gap between the code generated by the C/Fortran
systems, and the generated X10 code generated by MIX10. Furthermore, we found
that the MIX10 system using the X10 Java backend was often generating better code
than with the X10 C++ backend, which was counter-intuitive.
We determined that a key remaining problem was overhead due to casting doubles to
integers. This casting overhead was quite high, and was substantially higher for the
C++ back-end than for the Java back-end (since the casting instructions are handled
efficiently by the Java VM). This casting problem arises because the default data type
for MATLAB variables is double - even variables used to iterate through arrays, and
to index into arrays typically have double type, even though they hold integral values.
To tackle this issue we developed an IntegerOkay analysis which determines which
double variables can be safely converted to integer variables in the generated X10
code, hence greatly reducing the number of casting operations needed.
-
Open implementation:
- We have implemented the MIX10 compiler over various
MATLAB compiler tools provided by the McLAB toolkit. In the process we also
implemented some enhancements to these existing tools. Our implementation is
extensible and allows for others to make further improvements to the generated X10
code, or to reuse the analyses to generate code for other target languages.
-
Experimental evaluation:
- We have experimented with our MIX10 implementation on
a set of benchmarks. Our results show that our generated code is almost an
order of magnitude faster than the Mathworks’ standard JIT-based system, and
is competitive with other state-of-the-art tools that generate C/Fortran. Our more
detailed results show the importance of using our customized and optimized X10
array representations, and we demonstrate the effectiveness of the IntegerOkay
analysis. Finally, we show that our X10-based treatment of parfor significantly
outperforms MATLAB on our benchmarks.
1.2 Thesis Outline
This thesis is divided into 11 chapters, including this one and is structured as follows.
Chapter 2 provides an introduction to the X10 language and describes how it compares to
MATLAB from the point of view of language design. Chapter 3 gives a description of various
existing MATLAB compiler tools upon which MIX10 is implemented, presents a high-level
design of MIX10, and explains the design and need of MIX10 IR. In Chapter 4 we compare the
two kinds of arrays provided by X10, identify when each of them must be used in the generated
code, identify and address challenges involved in efficient compilation of MATLAB arrays.
Chapter 5 describes the builtin handling framework used by MIX10 to generate specialized code
for MATLAB builtins used in the source program. Chapter 6 gives a description of
efficient and effective code generation strategies for the core sequential constructs of
MATLAB. A description of code generation for the MATLAB parfor construct is
provided in Chapter 7, which also describes our strategy to introduce concurrency
constructs in MATLAB. In Chapter 8 we provide a description of the IntegerOkay analysis
to identify variables that are safe to be declared as Long type. Chapter 9 provides
performance results for code generated using MIX10 for a suite of benchmarks. It
gives a comparison between performance achieved by MIX10 generated code and
that generated by the MATLAB coder and MC2FOR compilers. Chapter 10 provides
an overview of related work and Chapter 11 concludes and outlines possible future
work.
Chapter 2
Introduction to the X10 Programming
Language
___________________________________________________________________________________
In this chapter, we describe key X10 semantics and features to help
readers unfamiliar with X10 to have a better understanding of the MIX10
compiler.
X10 is an award winning open-source programming language being developed by IBM
Research. The goal of the X10 project is to provide a productive and scalable programming
model for the new-age high performance computing architectures ranging from multi-core
processors to clusters and supercomputers [IBM12].
X10, like Java, is a class-based, strongly-typed, garbage-collected and object-oriented
language. It uses Asynchronous Partitioned Global Address Space (APGAS) model to support
concurrency and distribution [SBP+12]. The X10 compiler has a native backend that
compiles X10 programs to C++ and a managed backend that compiles X10 programs to
Java.
2.1 Overview of X10’s Key Sequential Features
X10’s sequential core is a container-based object-oriented language that is very similar to that of
Java or C++ [SBP+12]. An X10 program consists of a collection of classes, structs or interfaces,
which are the top-level compilation units. X10’s sequential constructs like if-else statements,
for loops, while loops, switch statements, and exception handling constructs throw and
try…catch are also same as those in Java. X10 provides both, implicit coercions and explicit
conversions on types, and both can be defined on user-defined types. The as operator is used to
perform explicit type conversions; for example, x as Long{self != 0} converts x to type
Long and throws a runtime exception if its value is zero. Multi-dimensional arrays in X10
are provided as user-defined abstractions on top of x10.lang.Rail, an intrinsic
one-dimensional array analogous to one-dimensional arrays in languages like C or Java. Two
families of multi-dimensional array abstractions are provided: simple arrays, which
provide a restricted but efficient implementation, and region arrays which provide a
flexible and dynamic implementation but are not as efficient as simple arrays. Listing 2.1
shows a sequential X10 program that calculates the value of π using the Monte Carlo
method.
It highlights important sequential and object-oriented features of X10 detailed in the following
subsections. It reads an argument from the console in an intrinsic 1 dimensions array(Rail) of
String and converts it to a Long value N. It then generates two random numbers and performs
computations on them in a loop from 1 to N. Finally, it calculates the value of π and displays the
result on the console.
X10’s syntax is similar to that of Java. The object-oriented semantics are also similar to that
of Java. Mutable and immutable variables are denoted by keywords var and val
respectively. for loops can iterate over a range of values. For e.g. in listing 2.1, the for loop
iterates over a LongRange of 1 to N. A LongRange represents a range of Long type
integers.
import x10.util.Random; public class SeqPi { public static def main(args:Rail[String]) { val N = Long.parse(args(0)); var result:Double = 0; val rand = new Random(); for(1..N) { val x = rand.nextDouble(); val y = rand.nextDouble(); if(x*x + y*y <= 1) result++; } val pi = 4*result/N; Console.OUT.println(~The value of pi is ~ + pi); } }
Listing 2.1:
Sequential
X10
program
to
calculate
value
of
π
using
Monte
Carlo
method
2.1.1 Object-oriented Features
A program consists of a collection of top-level units, where a unit is either a class, a struct or an
interface. A program can contain multiple units, however only one unit can be made public and
its name must be same as that of the program file. Similar to Java, access to these top-level units is
controlled by packages. Below is a description of the core object-oriented constructs in
X10:
-
Class
- A class is a basic bundle of data and code. It consists of zero or more members
namely fields, methods, constructors, and member classes and interfaces [IBM13b].
It also specifies the name of its superclass, if any and of the interfaces it implements.
-
Fields
- A field is a data item that belongs to a class. It can be mutable (specified by the
keyword var) or immutable (specified by the keyword val). The type of a mutable
field must be always be specified, however the type of an immutable field may
be omitted if it’s declaration specifies an initializer. Fields are by default instance
fields unless marked with the static keyword. Instance fields are inherited by
subclasses, however subclasses can shadow inherited fields, in which case the value
of the shadowed field can be accessed by using the qualifier super.
-
Methods
- A method is a named piece of code that takes zero or more parameters and
returns zero or one values. The type of a method is the type of the return value or
void if it does not return a value. If the return type of a method is not provided by
the programmer, X10 infers it as the least upper bound of the types of all expressions
e in the method where the body of the method contains the statement return e.
A method may have a type parameter that makes it type generic. An optional method
guard can be used to specify constraints. All methods in a class must have a unique
signature which consists of its name and types of its arguments.
Methods may be inherited. Methods defined in the superclass are available in
the subclasses, unless overridden by another method with same signature. Method
overloading allows programmers to define multiple methods with same name as
long as they have different signatures. Methods can be access-controlled to be
private, protected or public; private methods can only be accessed by
other methods in the same class, protected methods can be accessed in the same
class or its subclasses, and public methods can be accessed from any code. By
default, all methods are package protected which means they can be accessed from
any code in the same package.
Methods with the same name as that of the containing class are called constructors.
They are used to instantiate a class.
-
Structs
- A struct is just like a class, except that it does not support inheritance and may
not be recursive. This allows structs to be implemented as header-less objects, which
means that unlike a class, a struct can be represented by only as much memory as
is necessary to represent its fields and with its methods compiled to static methods.
It does not contain a header that contains data to represent meta-information about
the object. The current version of X10 (version 2.4) does not support mutability and
references to structs, which means that there is no syntax to update the fields of a
struct and structs are always passed by value.
-
Function literals
- X10 supports first-class functions. A function consists of a parameter
list, followed optionally by a return type, followed by =>, followed by the
body (an expression). For example, (i:Int, j:Int) => (i<j ? foo(i)
: foo(j)), is a function that takes parameters i and j and returns foo(i) if i<j
and foo(j) otherwise. A function can access immutable variables defined outside
the body.
2.1.2 Statements
X10 provides all the standard statements similar to Java. Assignment, if - else and while
loop statements are identical to those in Java.
for loops in X10 are more advanced and apart from the standard C-like for loop, X10
provides three different kinds of for loops:
-
- enhanced for loops take an index specifier of the form i in r, where r is any value that
implements x10.lang.Iterable[T] for some type T. Code listing 2.2 below shows
an example of this kind of for loops:
def sum(a:Rail[Long]):Long{ var result:Long = 0; for (i in a){ result += i; } return result; }
Listing 2.2:
Example
of
enhanced
for
loop
-
- for loops over LongRange iterate over all the values enumerated by a LongRange(a range
of consecutive Long type values). A LongRange is instantiated by an expression like
e1..e2 and enumerates all the integer values from a to b (inclusive) where e1 evaluates
to a and e2 evaluates to b. Listing 2.3 below shows an example of a for loop that uses
LongRange:
def sum(N:Long):Long{ var result:Long = 0; for (i in 0..N){ result += i; } return result; }
Listing 2.3:
Example
of
for
loop
over
LongRange
-
- for loops over Region allow to iterate over multiple dimensions simultaneously. A Region
is a data structure that represents a set of points in multiple dimensions. For instance, a
Region instantiated by the expression Region.make(0..5,1..6) creates a
2-dimensional region of points (x,y) where x ranges over 0..5 and y over
1..6. The natural order of iteration is lexicographic. Listing 2.4 below shows an
example that calculates the sum of coordinates of all points in a given rectangle:
def sum(M:Long, N:Long):Long{ var result:Long = 0; val R:Region = x10.regionarray.Region.make(0..M,0..N); for ([x,y] in R){ result += x+y; } return result; }
Listing 2.4:
Example
of
for
loop
over
a
2-D
Region
2.1.3 Arrays
In order to understand the challenges of translating MATLAB to X10, one must understand the
different flavours and functionality of X10 arrays.
At the lowest level of abstraction, X10 provides an intrinsic one-dimensional fixed-size array
called Rail which is indexed by a Long type value starting at 0. This is the X10 counterpart of
built-in arrays in languages like C or Java. In addition, X10 provides two types of more
sophisticated array abstractions in packages, x10.array and x10.regionarray.
-
Rail-backed Simple arrays
- are a high-performance abstraction for multidimensional
arrays in X10 that support only rectangular dense arrays with zero-based indexing.
Also, they support only up to three dimensions (specified statically) and row-major
ordering. These restrictions allow effective optimizations on indexing operations on
the underlying Rail. Essentially, these multidimensional arrays map to a Rail of
size equal to number of elements in the array, in a row-major order.
-
Region arrays
- are much more flexible. A region is a set of points of the same rank, where
Points are the indexing units for arrays. Points are represented as n-dimensional
tuples of integer values. The rank of a point defines the dimensionality of the array
it indexes. The rank of a region is the rank of its underlying points. Regions provide
flexibility of shape and indexing. Region arrays are just a set of elements with each
element mapped to a unique point in the underlying region. The dynamicity of these
arrays come at the cost of performance.
Both types of arrays also support distribution across places. A place is one of the central innovations
in X10, which permits the programmer to deal with notions of locality. places are discussed in
more detail in section 2.2.4
2.1.4 Types
X10 is a statically type-checked language: Every variable and expression has a type that is known
at compile-time and the compiler checks that the operations performed on an expression are
permitted by the type of that expression. The name c of a class or an interface is the most basic
form of type in X10. There are no primitive types.
X10 also allows type definitions, that allow a simple name to be supplied for a complicated
type, and for type aliases to be defined. For example, a type definition like public static
type bool(b:Boolean) = Boolean{self=b} allows the use of expression
bool(true) as a shorthand for type Boolean{self=true}.
-
Generic types
- X10’s generic types allow classes and interfaces to be declared parameterized by
types. They allow the code for a class to be instantiated unbounded number of times, for
different concrete types, in a type-safe fashion. For instance, the listing 2.5 below shows a
class List[T], parameterized by type T, that can be replaced by a concrete type like Int
at the time of instantiation (var l:List[Int] = new List[Int](item)).
class List[T]{ var item:T; var tail:List[T]=null; def this(t:T){ item=t; } }
X10 types are available at runtime, unlike Java(which erases them).
-
Constrained types
- X10 allows the programmer to define Boolean expressions (restricted)
constraints on a type [T]. For example, a variable of constrained type Long{self != 0}
is of type Long and has a constraint that it can hold a value only if it is not equal to 0 and
throws a runtime error if the constraint is not satisfied. The permitted constraints include the
predicates == and !=. These predicates may be applied to constraint terms. A constraint
term is either a final variable visible at the point of definition of the constraint, or the special
variable self or of the form t.f where f names a field, and t is (recursively) a constraint
term.
2.2 Overview of X10’s Concurrency Features
X10 is a high performance language that aims at providing productivity to the programmer. To
achieve that goal, it provides a simple yet powerful concurrency model that provides four
concurrency constructs that abstract away the low-level details of parallel programming from the
programmer, without compromising on performance. X10’s concurrency model is based on the
Asynchronous Partitioned Global Address Space (APGAS) model [IBM13a]. The APGAS model
has a concept of global address space that allows a task in X10 to refer to any object (local or
remote). However, a task may operate only on an object that resides in its partition of the address
space (local memory). Each task, called an activity, runs asynchronously parallel to each other. A
logical processing unit in X10 is called a place. Each place can run multiple activities. There are
four types of concurrency constructs provided by X10 [IBM13b], as described in the following
sections:
2.2.1 Async
The fundamental concurrency construct in X10 is async. The statement async S creates a new
activity to execute S and returns immediately. The current activity and the “forked" activity
execute asynchronously parallel to each other and have access to the same heap of objects as the
current activity. They communicate with each other by reading and writing shared variables.
There is no restriction on statement S in the sense that it can contain any other constructs
(including async). S is also permitted to refer to any immutable variable defined in lexically
enclosing scope.
An activty is the fundamental unit of execution in X10. It may be thought of as a very
light-weight thread of execution. Each activity has its own control stack and may invoke recursive
method calls. Unlike Java threads, activities in X10 are unnamed. Activities cannot be aborted or
interrupted once they are in flight. They must proceed to completion, either finishing
correctly or by throwing an exception. An activity created by async S is said to be
locally terminated if S has terminated. It is said to be globally terminated if it has
terminated locally and all activities spawned by it recursively, have themselves globally
terminated.
2.2.2 Finish
Global termination of an activity can be converted to local termination by using the finish
construct. This is necessary when the programmer needs to be sure that a statement S and all
the activities spawned transitively by S have terminated before execution of the next
statement begins. For instance in the listing 2.5 below, the use of finish ensures
that the Console.OUT.println(~a(1) = ~ + a(1)); statement is executed
only after all the asynchronously executing operations (async a(i) *= 2; have
completed.
//... //Create a Rail of size 10, with i’th element initialized to i val a:Rail[Long] = new Rail[Long](10,(i:Long)=>i); finish for (i in 0..9){ //asynchronously double every value in the Rail async a(i) *= 2; } Console.OUT.println(~a(1) = ~ + a(1)); //...
Listing 2.5:
Example
use
of
finish
construct
2.2.3 Atomic
The statement atomic S ensures that the statement S is executed in a single step with respect to
all other activities in the system. When S is being executed in one activity all other activities
containing s are suspended. However, the atomic statement S must be sequential (it should
not contain an async or finish staement), non-blocking (it should not contain a
blocking construct like when, explained below) and local (in this context, local means
place-local, that is, it must not contain an at construct, explained in Sec. 2.2.4). Consider
the code fragment in listing 2.6. It asynchronously adds Long values to a linked-list
list and simultaneously holds the size of the list in a variable size. The use of
atomic guarantees that no other operation, in any activity, is executed in between (or
simultaneously with) these two operations, which is necessary to ensure correctness of the
program.
//... finish for (i in 0..10){ async add(i); } //... def add(x:Long){ atomic { this.list.add(x); this.size = this.size + 1; } } //...
Listing 2.6:
Example
use
of
atomic
construct
Note that, atomic is a syntactic sugar for the construct when (c) , which is the conditional
atomic statement based on binary condition (c). Statement when (c) S executes statement S
atomically only when c evaluates to true; if it is false, the execution blocks waiting for c to be
true. Condition c must be sequential, non-blocking and local.
2.2.4 At
A place in X10 is the fundamental processing unit. It is a collection of data and activities that
operate on that data. A program is run on a fixed number of places. The binding of places to
hardware resources (e.g. nodes in a cluster, accelerators) is provided externally by a configuration
file, independent of the program.
The at construct provides a place-shifting operation, that is used to force execution of a
statement or an expression at a particular place. An activity executing at (p) S suspends
execution at the current place; The object graph G at the current place whose roots are all the
variables V used in S is serialized, and transmitted to place p, deserialized (creating a
graph G′ isomorphic to G), an environment is created with the variables V bound to the
corresponding roots in G′, and S executed at p in this environment. On local termination of S,
computation resumes after at (p) S in the original location. The object graph is
not automatically transferred back to the originating place when S terminates: any
updates made to objects copied by an at will not be reflected in the original object
graph.
2.3 Overview of X10’s Implementation and Runtime
In order to understand the compilation flow of the MIX10 compiler and enhancements made to
the X10 compiler for efficient use of X10 as a target language for MATLAB, it is important to
understand the design of the X10 compiler and its runtime environment.
2.3.1 X10 Implementation
X10 is implemented as a source-to-source compiler that translates X10 programs to
either C++ or Java. This allows X10 to achieve critical portability, performance and
interoperability objectives. The generated C++ or Java program is, in turn, compiled by
the platform C++ compiler to an executable or to class files by a Java compiler. The
C++ backend is referred to as Native X10 and the Java backend is called Managed
X10.
The source-to-source compilation approach in X10 provides three main advantages: (1) It
makes X10 available for a wide range of platforms; (2) It takes advantage of the underlying
classical and platform-specific optimizations in C++ or Java compilers, while the X10
implementation includes only X10 specific optimizations; and (3) It allows programmers to take
advantage of the existing C++ and Java libraries.
Figure 2.1 shows the overall architecture of the X10 compiler [IBM13b].
2.3.2 X10 Runtime
Figure 2.2 shows the major components of the X10 runtime and their relative hierarchy [IBM13b].
The runtime bridges the gap between application program and the low-level network transport
system and the operating system. X10RT, which is the lowest layer of the X10 runtime,
provides abstraction and unification of the functionalities provided by various network
layers.
The X10 Language Native Runtime provides implementation of the sequential
core of the language. It is implemented in C++ for native X10 and Java for Managed
X10.
XRX Runtime, the X10 runtime in X10 is the core of the X10 runtime system. It provides
implementation for the primitive X10 constructs for concurrency and distribution (async,
finish, atomic and at). It is primarily written in X10 over a set of low-level APIs that
provide a platform-independent view of processes, threads, synchronization mechanisms and
inter-process communication.
At the top of the X10 runtime system, is a set of core class libraries that provide fundamental
data types, basic collections, and key APIs for concurrency and distribution.
Chapter 3
Background and High-level Design of MIX10
___________________________________________________________________________________
3.1 Background
MIX10 is implemented on top of several existing MATLAB compiler tools. The overall structure
is given in Figure 3.1, where the new parts are indicated by the shaded boxes, and future work is
indicated by dashed boxes.
As illustrated at the top of the figure, a MATLAB programmer only needs to provide an
entry-point MATLAB function (called myprog.m in this example), plus a collection of other
MATLAB functions and libraries (directories of functions) which may be called, directly or
indirectly, by the entry point. The programmer may also specify the types and/or shapes of the
input parameters to the entry-point function. As shown at the bottom of the figure, our MIX10
compiler automatically produces a collection of X10 output files which contain the generated
X10 code for all reachable MATLAB functions, plus one X10 file called mix10.x10 which
contains generated and specialized X10 code for the required builtin MATLAB functions. Thus,
from the MATLAB programmer’s point of view, the MIX10 compiler is quite simple to
use.
MATLAB is actually quite a complicated language to compile, starting with its rather unusual
syntax, which cannot be parsed with standard LALR techniques. There are several issues that
must be dealt with including distinguishing places where white space and new line characters
have syntactic meaning, and filling in missing end keywords, which are sometimes
optional. The McLAB front-end handles the parsing of MATLAB through a two step
process. There is a pre-processing step which translates MATLAB programs to a cleaner
subset, called Natlab, which has a grammar that can be expressed cleanly for a LALR
parser. The McLAB front-end delivers a high-level AST based on this cleaner grammar.
After parsing, the next major phase of MIX10 uses the MCSAF framework [DH12a, Doh11]
to disambiguate identifiers using kind analysis [DHR11], which determines if an identifier refers
to a variable or a named function. This is required because the syntax of MATLAB does not
distinguish between variables and functions. For example, the expression a(i) could refer to four
different computations, a could be an array or a function, and i could refer to the builtin function
for the imaginary value i, or it could refer to a variable i. The MCSAF framework also
simplifies the AST, producing a lower-level AST which is more amenable to subsequent
analysis.
The next major phase is the Tamer [DH12b], which is a key component for any tool which
statically compiles MATLAB. The Tamer generates an even more defined AST called Tamer IR, as
well as performing key interprocedural analyses to determine both the call graph and an estimate
of the base type and shape of each variable, at each program point. The call graph is needed to
determine which files (functions) need to be compiled, and the type and shape information is very
important for generating reasonable code when the target language is statically typed, as is the
case for X10.
The Tamer also provides an extensible interprocedural value analysis and an interprocedural
analysis framework that extends the intraprocedural framework provided by MCSAF. Any static
backend will use the standard results of the Tamer, but is also likely to implement some
target-language-specific analyses which estimate properties useful for generating code in a
specific target language. Currently, we have implemented two analyses : (1) An analysis for
determining if a MATLAB variable is real or complex to enable support for complex numbers in
MIX10 and other MATLAB compilers based on McLAB; and (2) IntegerOkay analysis to identify
which variables can be safely declared to be of an integer type (Int or Long) instead of the
default type Double.
For the purposes of MIX10, the output of the Tamer is a low-level, well-structured
AST, which along with key analysis information about the call graph, the types and
shapes of variables, and X10-specific information. These Tamer outputs are provided to
the code generator, which generates X10 code, and which is the main focus of this
thesis.
The X10 source code generator actually gets inputs from two places. It uses the Tamer IR it
receives from the the Tamer to drive the code generation, but for expressions referring to
built-in MATLAB functions it interacts with the Built-in Handler which used the built-in
template file we provide. We describe the functioning of the built-in handler in Chapter
5.
Chapter 4 concentrates on generating efficient code for MATLAB arrays. Chapter 6
describes the code generation strategy for the sequential core of MATLAB, while Chapter 7
describes our strategy to generate parallel X10 code for MATLAB parfor construct, and
introducing X10 like concurrency constructs in MATLAB. The focus of this thesis is to
address challenges in generating efficient X10 code whose performance is comparable to
state-of-the-art tools that generate more traditional imperative languages like C and
Fortran.
3.2 High-level Design of the MIX10 Compiler
The MIX10 code generator is the key component which makes the translation from the Tamer IR,
which is based on MATLAB programming constructs and semantics, to X10. The overall structure
of the MIX10 code generator is given in Figure 3.2.
The input to to MIX10 compiler is the call graph generated by Tamer and the Tame IR
annotated with the necessary analysis information like shape, iscomplex, and type and
IntegerOkay. Rather than do a direct code generation to X10 source code, MIX10 translates the
Tamer IR to MIX10 IR, a general and extensible IR, designed by us, to represent X10. This
translation is done by the X10 IR generator module of MIX10. Finally, with the inputs from the
builtin handler and the X10 IR generator (after the X10 specific analyses and transformations
have been done), the X10 source code generator generates the resultatnt X10 source
code.
3.2.1 The MIX10 Intermediate Representation
The MIX10 IR is a low-level, three address like intermediate representation that is similar in
design to the Tamer IR and abstracts the X10 constructs while capturing the static
information required to generate the X10 source code. We have implemented the IR using
JastAdd [EH04, jas], which allows us to easily add new AST nodes by simply extending the
JastAdd specification grammar.
There are three important reasons to use an IR, instead of directly generating the X10
code:
- There are potentially two places that optimizations and transformations may happen:
either at the Tamer IR level or at the MIX10 IR level. It is our intent to put
any analysis or transformation that is not X10-specific into the Tamer IR, so that
other back-ends can benefit from those improvements. However, optimizations and
transformations that are specific to X10 programming constructs (such as points and
regions) and semantics will need to be done on the MIX10 IR. Although we currently
do not transform the MIX10 IR very much, the ultimate goal is to support a variety
of analyses and transformations that can be used to: (1) produce more efficient X10
code, and (2) produce more readable X10 code.
- There are X10 constructs that can be pretty printed to be of different kinds,
for example the X10 arrays, which can either be simple arrays, region arrays or
specialized region arrays, and X10 for loop which can either be C-like for loop
or an iterator over a LongRange (used in generated code for parfor loop). It
allows to abstract the vital information for a construct while leaving the actual syntax
to the source code generator. This makes it easier to add X10 specific analyses
and transformations, and makes it easy to update the compiler whenever a new or
improved variation of a construct is added.
- MIX10 IR can also be used as a convenient place to insert instrumentation code for
the generated X10 code.
Appendix B provides the JastAdd implementation of the MIX10 IR grammar.
Chapter 4
Techniques for Efficient Compilation of
MATLAB Arrays
___________________________________________________________________________________
Arrays are the core of the MATLAB programming language. Every value in MATLAB
is a Matrix and has an associated array shape. Even scalar values are represented as
1×1 arrays. Most of the data read and write operations involve accessing individual or
a set of array elements. Given the central role of arrays in MATLAB, it is of utmost
importance for our MIX10 compiler to find effective and efficient translations to X10
arrays.
Given the shape information provided by the shape analysis engine [LH14] built
into the McLAB analysis framework [DH12a, Doh11, DH12b], it was not hard to
compile MATLAB arrays to X10. However, to generate X10 code whose performance
would be competitive to the generated C code (via MATLAB coder) and the generated
Fortran code (via the MC2FOR compiler), was not straightforward, and required deeper
understanding of the X10 array system and careful handling of several features of the MATLAB
arrays.
4.1 Simple Arrays or Region Arrays
As described in Section 2.1.3, X10 provides two higher level abstractions for arrays, simple
arrays, a high performance but rigid abstraction, and region arrays, a flexible abstraction but not as
efficient as the simple arrays. In order to achieve more efficiency, our strategy is to use the simple
arrays whenever possible, and to fall back to the region arrays when necessary. Note that it is
possible to force the MIX10 compiler to use region arrays via a switch, for experimentation
purposes.
4.1.1 Compilation to Simple Arrays
In dealing with the simple rail-backed arrays, there were two important challenges. First, we
needed to determine when it is safe to use the simple rail-backed arrays, and second, we needed
an implementation of simple rail-backed arrays that handles the column-major, 1-indexing, and
linearization operations required by MATLAB.
When to use simple rail-backed arrays:
After the shape analysis of the source MATLAB program, if shapes of all the arrays in the
program: (1) are known statically, (2) are supported by the X10 implementation of simple arrays
and (3) the dimensionality of the shapes remain same at all points in the program; then MIX10
generates X10 code that uses simple arrays.
Column-major indexing:
In order to make X10 simple arrays more compatible with MATLAB, we modified the implementation
of the Array_2 and Array_3 classes in x10.array package to use column-major ordering instead
of the default row-major ordering when linearizing multidimensional arrays to the backing Rail
storage.http://www.sable.mcgill.ca/mclab/mix10/x10_update/
Since MATLAB uses column-major ordering to linearize arrays, this modification
also makes it trivial to support linear indexing operations in MATLAB.
http://www.mathworks.com/help/matlab/math/matrix-indexing.html
MATLAB naturally supports linear indexing for individual element access. More precisely, if the
number of subscripts in an array access is less than the number of dimensions of the array, the last
subscript is linearly indexed over the remaining number of dimensions in a column-major fashion.
Our modification to use column-major ordering for the backing Rail make it easier and more
efficient to support linear indexing by allowing direct access to the underlying Rail at the
calculated linear offset.
Given that we can determine when it is safe to use the simple rail-backed arrays,
and our improved X10 implementation of them, we then designed the appropriate
translations from MATLAB to X10, for array construction, array accesses for both individual
elements and ranges. Given the number of dimensions and the size of each dimension, it is
easy to construct a simple array. For example a two-dimensional array A of type T and
shape m×n can be constructed using a statement like val A:Array_2[T] = new
Array_2[T](m,n);. Additional arguments can be passed to the constructor to initialize the
array. Another important thing to note is that MATLAB allows the use of keyword end or an
expression involving end (like end-1) as a subscript. end denotes the highest index
in that dimension. If the highest index is not known the numElems_i property of
the simple arrays is used to get the number of elements in the ith dimension of the
array.
4.1.2 Compilation to Region Arrays
With MATLAB’s dynamic nature and unconventional semantics, it is not always possible to
statically determine the shape of an arrays accurately. Luckily, with some thought to
a proper translation, X10’s region arrays are flexible enough to support MATLAB’s
“wild" arrays. Also, since Point objects can be a set of arbitrary integers, there is no
restriction on the starting index of the arrays. Region arrays can easily use one-based
indexing.
Array construction:
Array construction for region arrays involves creating a region over a set of points (or index
objects) and assigning it to an array. Regions of arbitrary ranks can be created dynamically. For
example, consider the following MATLAB code snippet:
function[x] = foo(a) t = bar(a); x = t; ... end
function[y] = bar(a) if (a == 3) y = zeros(a,a+1,a+2,a+3); else y = zeros(a,a+1,a+2); end end
In this code, the number of dimensions of array t and hence array x cannot be determined
statically at compile-time. In such case, it is not possible to generate X10 code that uses
simple arrays, however, it can still be compiled to the following X10 code for function
foo().
static def foo(a: Double){ val t: Array[Double] = new Array[Double](bar(a)); val x: Array[Double] = new Array[Double](t); ... return x; }
static def bar(a:Double){ var y:Array[Double]=null; if (a == 3) { y = new Array[Double] (Mix10.zeros(a,a+1,a+2,a+3)); } else { y = new Array[Double] (Mix10.zeros(a,a+1,a+2)); } return y; }
In this generated X10 code, t is an array of type Double which can be created by copying
from another array returned by bar(a) without knowing the shape of the returned
array.
Array access:
Subscripting operations to access individual elements are mapped to X10’s region array
subscripting operation. If the rank of array is 4 or less, it is subscripted directly by integers
corresponding to subscripts in MATLAB otherwise we create a Point object from these integer
values and use it to subscript the array. In case an expression involving end is used for indexing
and the complete shape information is not available, method max(Long i), provided by the
Region class is used, allowing to determine the highest index for a particular dimension at
runtime.
Rank specialization:
Although region arrays can be used with minimal compile-time information, providing
additional static information can improve performance of the resultant code by eliminating
run-time checks involving provided information. One of the key specializations that we
introduced with use of region arrays is to specify the rank of an array in its declaration, whenever
it is known statically. For example if rank of an array A of type T is known to be two, it can be
declared as val A:Array[T](2);. This specialization provided better performance
compared to unspecialized code as shown in section 9.6.
4.2 Handling the Colon Expression
MATLAB allows the use of an expression such as a:b (or colon(a,b)) to create a vector of
integers [a, a+1, a+2, ... b]. In another form, an expression like a:i:b can be used to
specify an integer interval of size i between the elements of the resulting vector. Use of a
colon expression for array subscripting takes all the elements of the array for which the
subscript in a particular dimension is in the vector created by the colon expression in that
dimension.
Consider the following MATLAB code:
function [x] = crazyArray(a) y = ones(3,4,5); x = y(1,2:3,:); end
Here y is a three-dimensional array of shape 3×4×5 and x is a sub-array of y of shape 1×2×5.
Such array accesses can be handled by simply calling the getSubArray[T]() that we have
implemented in a Helper class provided with the generated code. The generated X10 code with
simple array for this example is as follows:
static def crazyArray (a: Double){ val y: Array_3[Double] = new Array_3[Double](Mix10.ones(3, 4, 5)); val mc_t0: Array_1[Double] = new Array_1[Double](Mix10.colon(2, 3)); var x: Array_3[Double]; x = new Array_3[Double](Helper.getSubArray(1, 1, mc_t0(0), mc_t0(1), 1, 5, y)) ; return x; }
The colon operator can also be used on the left hand side for an array set operation that
updates multiple values of the array. For example, in the MATLAB statement x(:,4) = y;, all
the values of the fourth column of x will be set to y if y is a scalar or to corresponding values of y
if y is a column vector with length equal to the size of first dimension of x. To handle this kind of
operation we have implemented another helper method, setSubArray(). This method takes as
input, the target array, the bounds on each dimension, and the source array. x(:,4) = y; will be
translated by MIX10 to x = Helper.setSubArray(x, 1, x.numElems_1, 4, 4,
y);
We have implemented overloaded versions of the getSubArray() and the
setSubArray() methods for arrays of different dimensions. For region arrays, we provide the
same methods that operate on region arrays in a different version of the Helper class.
MIX10 provides the correct version of the Helper class, based on what kind of arrays are
used.
4.3 Array Growth
MATLAB allows explicit array growth during runtime via the horzcat() and the vertcat()
builtin functions for array concatenation operations. In MIX10 this feature is supported for
simple arrays as long as the array growth does not change the number of dimensions of the array.
For region arrays, this feature is supported in full. For simple arrays, X10 allows a variable
declared to be an array of rank i, to hold any array value of the same rank. For example, consider
the following set of statements:
//... var x:Array_2[Long]; x = new Array_2(3,4,0); y = new Array_2(3,5,0); x=y; //...
Here, x is defined to be of type Array_2[Long] and can hold arrays of different sizes at
different points in the program.
Region arrays, being more dynamic, also support array growth even if it changes the rank of
the array. For example, the following set of statements are valid in an X10 program that uses
region arrays:
//... var x:Array[Long]; x = new Array(Region.make(1..3,1..4),0); y = new Array(Region.make(1..3,1..5,1..6),1); x=y; //...
Here x is a 2-dimensional array and y is a 3-dimensional array.
Section 9.6 discusses the performance results obtained by using different kinds of arrays and
provides a comparison of them, thus showing the efficiency of our approach for compiling
MATLAB arrays to X10.
Chapter 5
Handling MATLAB Builtins
___________________________________________________________________________________
MATLAB builtin methods are the core of the language and one of the features that make it
popular among scientists. They provide a huge set of commonly used numerical functions. All the
operators, including the standard binary operators (+, -, *,/), comparison operators
(<, >, <=, >=, ==) and logical operators (&, &&, |, ||) are merely syntactic sugar for
corresponding builtin methods that take the operands as arguments. For example an expression
like a+b is actually implemented as plus(a,b). An important thing to note is that unlike most
programming languages, all the MATLAB builtin methods by default operate on matrix values as a
whole. For example a*b or mtimes(a,b) actually performs matrix multiplication on matrix
values a and b. However, most of the builtin methods also accept one or more scalar, or more
accurately, 1×1 matrix arguments. Builtin methods are overloaded to accept almost all
possible shapes of arguments. Thus mtimes(a,b) can have both a and b as matrix
arguments (including 1×1 matrices) with number of columns in a equal to number
of rows in b, in which case the result is a matrix multiplication of a and b or one of
them can be a 1×1 matrix and other can be a matrix of any size and the result is a
matrix containing each element of the non-scalar argument times the scalar argument.
Wherever possible, MATLAB builtins also support complex numerical values. X10 on
the other hand, like most of the programming languages operates on scalar values by
default.
Due to the fact that X10 is still new and evolving, it has a very limited set of libraries,
specially to support a large subset of available MATLAB builtin methods. The X10 Global Matrix
Library (GML) supports double-precision matrix operations however it is still not as extensive as
MATLAB’s set of operations and it poses some restrictions:
- It works on values of type Matrix instead of X10 type Array which means it
needs explicit conversion of Array values to Matrix values before performing a
matrix operation and and then a conversion of the results back to Array type. This
conversion may be a large overhead, especially for small data sizes.
- GML is limited to Matrix values of two dimensions and containing elements of type
Double, whereas many MATLAB builtin methods support values of greater number
of dimensions.
- GML currently does not support complex numerical values whereas MATLAB
naturally supports them.
- Currently GML requires a separate installation and configuration which is non-trivial
specially for scientists who need something that works out of the box.
Due to above restrictions, X10 Global Matrix Library is useful in some situations, for
example when there is a matrix multiplication of a very large data size, but cannot be used or is
not a good choice for a large number of operations.
For a language with open-sourced libraries, it would be possible to actually compile the
library methods to X10. However, many MATLAB libraries are closed source and thus it is not
possible to translate them to X10.
5.0.1 The MIX10 Builtin Support Framework
We decided to write our own X10 implementations of the commonly used MATLAB
builtin methods. Currently we have implemented only those methods that are used in our
benchmarks. In this thesis, we concentrate on how these methods are included in the
generated X10 code with minimal loss of readability and performance rather than the actual
implementation.
The code below shows the X10 code for the MATLAB builtin method plus(a,b) involving
2-dimensional simple arrays.
public static def plus(a: Array_2[Double], b:Array_2[Double]){ val x = new Array_2[Double](a.numElems_1, a.numElems_2); for (p in a.indices()){ x(p) = a(p)+ b(p); } return x; } public static def plus(a:Double, b:Array_2[Double]){ val x = new Array_2[Double](b.numElems_1, b.numElems_2); for (p in b.indices()){ x(p) = a+ b(p); } return x; } public static def plus(a:Array_2[Double], b:Double){ val x = new Array_2[Double](a.numElems_1, a.numElems_2); for (p in a.indices()){ x(p) = a(p)+ b; } return x; } public static def plus(a:Double, b:Double){ val x: Double; x = a+b; return x; }
This X10 code contains four overloaded versions (and it still does not contain methods to
support complex values, variables of types other than Double, simple arrays of other dimensions,
and region arrays) based on whether the arguments are scalar or Array_2 and their relative
position in the list of arguments.
Including all the overloaded versions and versions specialized for arrays of different
dimensions or region arrays, in the generated X10 code would result in lot of lookup overhead,
would require producing redundant code (versions of methods with arguments of similar shape
but different types will have the same algorithm) and would generate large code with less
readability. Instead we designed a specialization technique that selects the appropriate
versions of only the methods used in the source MATLAB program. Note that the use of
generic types to handle arguments of different types is not always a good idea, since
several builtin implementations involve calls to X10 library functions which are not
defined on generic types. For example, functions in the x10.lang.Math librarry like
floor(Double a), max(Double a, Double b), etc. do not take generic type
arguments.
After studying numerous builtin methods we categorized them into the following five
categories:
-
Type 1:
- All the parameters are scalar values or no parameters.
-
Type 2:
- All the parameters are arrays.
-
Type 3:
- First parameter is scalar, rest of the parameters are arrays.
-
Type 4:
- Last parameter is scalar, rest of the parameters are arrays.
-
Type 5:
- Any other type(Default).
Each of these categories, except Type 5, uses similar code template for different types of
values. Note that due to the three address code-like structure of Tame IR, any call to a builtin
almost always contains zero, one or two arguments. For builtin calls like horzcat
and vertcat which may contain variable number of arguments, MIX10 packs all
the arguments in a Rail and passes a single argument of type Rail. Accordingly,
these builtins are implemented in Type 2 category and receive a single argument of type
Rail.
We build an XML file that contains the method bodies for each category for every builtin
method (that we support). The XML also contains specialized implementations of every builtin
for different kinds of arrays. We implement the following strategy to select and generate the
correct and required methods. First, we make a pass through the AST to make a list of all the
builtin methods used in the source MATLAB program. Next, we parse the XML file
once and read in the X10 code templates for all the categories of the builtin methods
collected in the first step. Next, whenever a call to a builtin method is made, based on the
results of the value analysis we: (1) Identify the required specialization for the method
(simple array or region array); and (2) generate the correct method header and select
the corresponding builtin template in the required specialization for that method. The
generated methods are finally written to a X10 class file named Mix10.x10. In the
code generated for actual MATLAB program, the call to a builtin method is simply
replaced by a call to the corresponding method in the Mix10 class. For example, MATLAB
expression plus(a,b) is translated to X10 expression Mix10.plus(a,b). Appendix A
demonstrates the structure of the builtin XML with an example implementation of the builtin
plus.
Using the above approach not only improves the readability of the generated code, but it also
allows for future extensibility, better maintenance and more specialization. Specializations that we
plan to add in future are: (1) the ability to use the Global Matrix Library for the available methods
in it and whenever the data size is large enough; and (2) concurrent versions of the relevant
builtins to support the execution of vector instructions in parallel fashion, as described in
section 7.3. We also encourage advanced users to mdoify the generated Mix10.x10 file
to enhance or add builtin implementations for higher performance of the generated
code.
Chapter 6
Code Generation for the Sequential Core
___________________________________________________________________________________
MATLAB is a programming language designed specifically for numerical computations. Every
value is a Matrix and has an associated array shape. Even scalar values are 1×1 matrices. Vectors
are 1×n or n×1 matrices. All the values are by default of type double. MATLAB naturally
supports imaginary components for all numerical values and almost all operators and library
functions support complex inputs. In the rest of this chapter we describe some of the key features
of MATLAB that demonstrate what makes MATLAB different and challenging to compile
statically and techniques used by MIX10 to translate these “wild" features to X10. We provide
necessary details on the various MATLAB constructs as we discuss them, however for the readers
who are totally unfamiliar with MATLAB, we suggest reading chapter 2 of the M.Sc. thesis on the
Tamer framework [Dub12].
6.1 Methods
A function definition in MATLAB takes one or more input arguments and returns one or more
values. A typical MATLAB function looks as follows:
function[x,y] = foo(a,b) x = a+3; y = b-3; end
This function has two input arguments a and b that can be of any type and any shape and
returns two values x and y of the same shape as a and b respectively and of types determined by
MATLAB’s type conversion rules. The Tamer IR provides a list of input arguments and a list of
return values for a function. The interprocedural value analysis identifies the types, shapes
and whether they are complex numerical values for all the arguments and the return
values.
MATLAB functions are mapped to X10 methods. If it is the entry function, the type of the
input argument is specified by the user (Tame IR requires to have an entry function or a driver
function with one argument. This function may call other functions with any number of input
arguments). For other functions the parameter types are computed by the value analysis
performed by the Tamer on the Tame IR. The type information computed includes the type of the
value, its shape and whether it is a complex value. Other statements in the function block are
processed recursively and corresponding nodes are created in the X10 IR. Finally, if there are
any return values, as determined by the Tame IR, a return statement is inserted in the
X10 IR at the end of the method. If the function returns only one value, say x then the
inserted statement is simply return x; but if the function returns more than one
values (which is quite common in MATLAB) then we return a Rail of type Any whose
elements are the values that are returned. So, for the above example the return statement is
return [x as Any, y as Any];. Note that the use of short syntactic form for Rail
construction improves the readability of the generated code. Below is the generated code for the
simple example above.
static def foo(a: Double, b: Double){ var mc_t0: Double = 3.3; var x: Double = Mix10.plus(a, mc_t0); var mc_t1: Double = 3.2; var y: Double = Mix10.minus(b, mc_t1); return [x as Any, y as Any]; }
Also note that the variables mc_t0 and mc_t1 are introduced by Tamer in the Tame
IR.
6.2 Types, Assignments and Declarations
MATLAB provides following basic types:
- double, single: floating point values
- uint8, uint16, uint32, uint64: unsigned integer values
- int8, int16, in32, int64: integer values
- logical: boolean values
- char: character values (strings are vectors of char)
These basic types are naturally mapped to X10 base types as follows. Floating point values
are mapped to Double and Float respectively, unsigned integers are mapped to
UByte, UShort, UInt and ULong, integer values are mapped to Byte, Short, Int
and Long, logical is mapped to Boolean and char is mapped to Char (vector of chars is
mapped to String type). If the shape of an identifier of type T is greater than 1×1 it is mapped
to Array[T]. The type conversion rules are quite different from standard languages. For
example, an operation involving a double and an int32 results in a value of type
int32.The type rules are explained in detail in the Tamer documents, www.sable.mcgill.ca/mclab/tamer.html.
MIX10 inserts an explicit typecast wherever required.
All the MATLAB operators are designed to work on matrix values and are provided as
syntactic sugar to the corresponding builtin methods that take operands as arguments. Operators
are overloaded to support different semantics for 1×1 matrices (scalar values). MATLAB provides
two types of operators - matrix operators and array operators. Matrix operators work on whole
matrix values. These include matrix multiplication (*) and matrix division (\, /). Array operators
always operate in an element-wise manner. For example array multiply operator .* performs
element-wise multiplication. As described in Chapter 5, MIX10 implements all operators as
builtins.
MATLAB is a dynamically typed language which means that variables need not be declared
and take up any value that they are assigned to. X10 however, is statically typed and requires
variables to be declared before being assigned to. MIX10 maintains a list of all the declared
variables. It starts with an empty list. Whenever an identifier appears in an assignment statement
on LHS, if it is not already present in the list, a declaration statement is added to the X10 IR and
the variable (with its associated type and value information) is added to the list, followed by an
assignment statement corresponding to the statement in MATLAB. If the identifier is
already present in the list, the assignment statement is added to the X10 IR and the
associated type and value information is updated. In case the MATLAB assignment
statement is inside a loop and needs a declaration, the declaration statement (without any
assignment) is added to the method block outside any loop or conditional scope and
the assignment statement is added in the scope where it is present in MATLAB code.
If the identifier on LHS is an array, then the declaration creates a new array with the
shape corresponding to the shape of the RHS array. For example a MATLAB statement
like a=b; where shape of a is, say, 3×3 and type is double will be translated to
a:Array_2[Double]=new Array_2[Double](b); for simple arrays and
a:Array[Double]=new Array[Double](b); for region arrays (outside the scope of
any loops or conditionals).
6.3 Loops
Loops in MATLAB are fairly intuitive except for one semantic difference from most of the
languages. In a for loop if the loop index variable is redefined inside the body of the loop, then
its new value is persistent only in a particular iteration and does not affect the number of loop
iterations. For example, consider the following listing.
function [x] = forTest1(a) for i = (1:10) i=3; a=a+i; end x=a; end
Note that inside every iteration, the value of loop index variable i is 3 but the loop still
terminates after ten iterations. The above code would be translated to the following X10
code:
static def forTest1 (a: Double) { //Note that in the actual generated code //the name of the temporary variable introduced by MiX10 //is mangled to ensure that there is no //conflict with any other variable name. var mc_t0: Long = 1; var mc_t1: Long = 10; var i_x10: Long; var b: Double; var i: Long; for (i_x10 = mc_t0; (i_x10 <= mc_t1); i_x10 = (i_x10 + 1)) { i = i_x10; i = 3 ; b = Mix10.plus(a, i) ; } var x: Double = a; return x; }
To handle this somewhat different semantics we introduce a new loop index variable and
assign it to the original loop index variable at the beginning of the loop body. The rest of the loop
body is translated by standard rules. Note that the new loop index variable is introduced only if
the actual loop index variable is redefined inside the loop body.
6.4 Conditionals
In MATLAB conditionals are expressed using the if-elseif-else construct and do not have any wild
semantics. MATLAB also allows switch statements which are converted to equivalent if-else
statements by the Tamer. It also recursively converts a statement like if (B1) S1 elseif
(B2) S2 else S3 to a series of if-else clauses like if (B1) S1 else{ if(B2)
S2 else S3}. This if-else construct is intuitively mapped to the if-else construct in
X10.
6.5 Function Calls
Function calls in MATLAB are similar to other programming languages if the called function
returns nothing or returns only one value. However, MATLAB allows a function to
return multiple values. Whenever a call is made to such a function, returned values are
received in a list in the order specified by function definition. For example in the statement
[x,n] = bubble(a); a call is made to the function bubble which returns two values that
are read into x and n respectively. This statement is compiled to following code in
X10.
//Note that in the actual generated code //the name of the temporary variable introduced by MiX10 //is mangled to ensure that there is no //conflict with any other variable name. var x: Double; var n: Double; val _x_n: Rail[Any]; _x_n = bubble(A) ; x = _x_n(0) as Double ; n = _x_n(1) as Double ;
The key idea here is to create a Rail of type Any and read the returned value. Remember that
MIX10 packs the multiple return values of a method in a Rail of type Any and returns it.
Individual elements of the list simply read the values from this array. If the function call is inside a
loop, all the declarations are moved out of the loop and only assignments are inside the
loop.
6.6 Cell Arrays
Cell arrays in MATLAB are arrays of data containers called cells and each cell can contain data of
any type. For example fooCell = {’x’,10,’I like’,ones(3,3)}; creates a cell
array containing values of type char, double, char array and a double array. To convert
to X10, the elements of the cell array are packed into a rail of type Any. While
accessing an element it is type cast into its original type. Consider the following MATLAB
listing:
function [x] = cellTest(a) m = ones(2,3); n = [4,5]; myCell = {m, n*100}; x = myCell{1,2}; end
It creates a cell array containing two arrays. It is translated to the below X10 code:
static def cellTest (a: Double) { //Note that for the purpose of demonstration, //this example uses region arrays and //does not use IntegerOkay analysis. var mc_t2: Double = 2; var mc_t3: Double = 3; var m: Array[Double] = new Array[Double](Mix10.ones(mc_t2, mc_t3)); var mc_t5: Double = 4; var mc_t6: Double = 5; var n: Array[Double] = new Array[Double](Mix10.horzcat(mc_t5, mc_t6)); var mc_t0: Array[Double] = new Array[Double](m); var mc_t7: Double = 100; var mc_t1: Array[Double] = new Array[Double](Mix10.mtimes(n, mc_t7)); var myCell: Rail[Any] = [mc_t0 as Any ,mc_t1 as Any]; var mc_t9: Double = 1; var mc_t10: Double = 2; var x: Array[Double]; x = myCell(mc_t9 as Long -1, mc_t10 as Long -1) as Array[Double]; return x; }
Chapter 7
Code Generation for Concurrency in MATLAB
___________________________________________________________________________________
MATLAB programmers often recognize the parallel nature of computations involved in their
programs but cannot express it due to the lack of fine-grained concurrency controls in MATLAB.
Some concurrency can be achieved using controls like parfor and other tools in Mathwork’s
parallel computing toolbox, but this has several drawbacks: (1) the parallel toolbox is limited in terms
of scaling (MATLAB currently supports only up to 12 workers processes to execute applications
on a multicore processor [Mat13]); (2) the parallel toolbox must be purchased separately, so not
even all licensed MATLAB users will have it available; and (3) MATLAB’s concurrency is often
slower compared to X10’s concurrency controls (as shown in section 9.8). Vectorization
http://www.mathworks.com/help/matlab/matlab_prog/vectorization.html is
a technique to convert loop-based scalar operations to vector operations, for which
MATLAB is optimized. So, another way of exposing parallelism in MATLAB is to optimize
these instructions to perform the computations concurrently on the elements of the
vector.
Sec. 2.2 gives an introduction to the concurrency controls in X10. Readers not familiar with
X10 may find it useful to read it before continuing with this chapter.
7.1 Code Generation for the MATLAB parfor Loop Construct
The MATLAB parfor construct is an important feature in MATLAB and is provided by the
Mathworks’ parallel computing toolbox [Mat13]. It allows the for loop iterations in the
MATLAB programs to be executed in parallel, whenever safely possible, thus greatly
enhancing the performance of the for loop execution. Other static MATLAB compilers like
MATLAB coder and MC2FOR do not support the parfor loop due to the lack of builtin
concurrency features in their target languages, C and Fortran. However, X10, being
a parallel programming language, naturally provides concurrency control features.
The MIX10 compiler supports parallel code generation for the MATLAB parfor
construct and provides significantly better performance compared to MATLAB code
with parfor, and also the sequential version of the X10 code generated for the same
program.
The parfor (or parallel for loop) is a key parallelization control provided by the MATLAB
parallel computing toolbox that can be used to execute each iteration of the for loop in parallel
with each other. The challenge was to implement it with X10’s concurrency controls while
maintaining its complex semantics and aiming for better performance than provided by the
parallel computing toolbox. There are three important semantic characteristics of MATLAB’s
parfor loop:
- the scope of variables inside a parfor loop, including the loop index variable, is
limited to each iteration.
- if a variable defined outside the loop is modified inside the loop such that its value
after the loop is dependent on the sequence of execution of iterations, then its value
after the loop is set to its value before the loop.
- if a variable defined outside the loop is modified in a reduction assignment i.e., the
final value after the iterations is independent of the order of execution of iterations,
the updated value is retained after the parfor loop. Consider the MATLAB code
given on the left of Figure 7.1.
Here x = x+i; is a reduction assignment [Matb] statement. The value of d is local to
each iteration and the initial value before the loop is retained after the loop. Note that the
value of d outside the loop is invisible inside the loop. For statement A(i) = d;,
each iteration modifies a unique element accessible only to it, hence the final
value of A is independent of order of execution; thus its value is updated after the
loop.
The MIX10 compiler uses the following strategy to translate parfor loops to
X10:
- Introduce finish and async constructs to control the flow of statements in
parallel. This puts the statement immediately after the for loop in wait, until all the
iterations have been executed.
- Any variable defined inside the loop and not declared outside the loop previously is
declared inside the async scope to make it local to the iteration.
- Any variable defined inside the loop that is previously defined outside the loop and is
not a reduction variable is replaced by a local temporary variable defined inside the
loop.
- Statements identified to be reduction statements are made atomic by using the
atomic construct in X10.
An equivalent X10 code for the above example MATLAB code is given on the right side of
Figure 7.1. The use of finish and async ensure that each iteration is executed in parallel and
the statement after the for loop is blocked until all the iterations have finished executing. Note
that the for loop is iterated over a LongRange to ensure that the declaration of the loop variable
i is local to each iteration. The statement x = x+i is a reduction statement, since its order of
execution does not affect the value of x at the end of the loop. It is declared to be atomic to
ensure that the two operations of addition and assignment in the statement are executed as a
whole, without any interference from its execution in other iterations. Since the variable d is also
defined outside the loop, it is replaced by a local variable d_local inside the loop.
Finally, since each array variable A(i) is unique, it is executed normally for each
iteration.
To conclude, we can translate the parfor in MATLAB to semantically equivalent
code in X10 and since X10 can handle massive scaling, we can get significantly better
performance for X10 compared to MATLAB as shown by our experimental results in Section
9.8.
7.2 Introducing Concurrency Controls in MATLAB
In order to enable MATLAB to be compiled for high performance computing it is important to let
programmers exploit fine-grained concurrency in their MATLAB programs. Due to the lack of
fine-grained concurrency controls in traditional MATLAB, we decided to introduce such controls
in MATLAB that can be translated by our MIX10 compiler to analogous concurrency controls in
X10. However it was important that introduction of such controls should not have any side-effects
when compiled by traditional Mathworks’ MATLAB compiler, so we introduced them as
structured special comments.
We introduced the following concurrency constructs in MATLAB: (1) %!async, (2)
%!finish, (3) %!atomic, (4) %!when(condition) (5) (where condition is a
boolean expression) and (6) %!at(p) (where p is an integer value denoting a place in
X10). Programmers can express these constructs before the statements that they want to
control and specify the end of a control by using %!end after the statements. Note that
because of the preceding % sign these constructs will be treated like comments by other
MATLAB compilers and will not cause any unwanted effects. It is important to note that the
MATLAB programmer, using these constructs in her program, must ensure that the
parallel execution caused by the use of these constructs does not change the behavior of
the program from that of the sequential execution of the program. In short, it is the
responsibility of the programmer to ensure the safety of the program when using these
constructs.
Figure 7.2 shows an example of how to use these controls in MATLAB followed by the
generated X10 code for it.
7.3 Parallelizing Vectorized Instructions
The use of vectorized instructions is another optimization technique used by MATLAB to speedup
single operations on multiple scalar values by combining scalar values in a vector and executing
the operation on the vector. Such Single instruction, multiple data style operations are good
candidates for parallelization. However, efficiency of parallelization of such operations
depends on the size of the vector, the complexity of the operation involved, and the
executing hardware. Thus, in order to make it most effective, we wanted to provide full
support for parallelization of vector instructions and give the programmer the ability to
control when the vector operation is executed concurrently, based on the size of the
vector.
We implemented a concurrent version of the relevant builtin
operations that can operate in a parallel fashion on vectors of arbitrary
sizes.Currently, these concurrent builtin implementations are not integrated into the builtin handling framework.
However, due to the extensible nature of the builtin handling framework, it should be straightforward to add a
specialization for a concurrent version of the builtins. We plan to do it as a future work.
We also introduced a compiler switch for MIX10 that lets programmers specify a vector length
threshold for all builtins or a specific builtin above which the concurrent version of the builtin will
be executed. For example, if the user wants an operation sin(A) to be executed concurrently
only if A is a vector of length greater than, say, 1000; then while invoking the MIX10 compiler
she can specify the threshold by using the switch -vec_par_length sin=1000. MIX10
will generate a call to the concurrent version of sin() if the length of A is greater than
1000 else it will call the sequential version. Using the -vec_par_length switch
programmer can specify threshold for one or more or all builtin methods. For example
-vec_par_length all=500 sin=1000 cos=1000 will set the threshold for sin()
and cos() to 1000 and to 500 for all other builtins.
As a future work, we plan to extensively evaluate the concurrent execution for the vectorized
instructions. It would be interesting to study the performance variations of concurrently executing
vector instructions, with varying threshold vector length values and on different parallel
architectures.
Chapter 8
The IntegerOkay Analysis
___________________________________________________________________________________
In this chapter we present the IntegerOkay analysis to identify which variables in the source
MATLAB program can be safely declared to be of an integer type instead of the default double
type. In MATLAB all the variables holding a numerical value are by default of type Double,
which means that by default, in the X10 code generated from MATLAB, all variables are statically
declared to be of Double. However, in languages like X10, Java and C++, certain program
operations require the variables used to be of an integer type. A prominent example of such
an operation is an array access operation. An array access requires the variables used
to index into the array to be of an integer type. For example, in a statement like x =
A(i,j), the variables i and j are required to be of integer type and result in an error
otherwise.
8.1 Need for Declaring Variables to be of Integer Type
A simple solution to handle this problem in the generated code from MATLAB is to
explicitly cast the variable from Double to Long, whenever it is required to be used as an
integer. However, our experiments showed this approach to be very inefficient. With this
approach, we observed that the C++ programs generated by the X10 compiler’s C++
backend were slow, and often even slower than the Java code generated by the X10 Java
backend for the same program (which was somewhat surprising). The reason for the
added slowness in the C++ code was because each typecast from Double to Long
involved an explicit check on the value of the Double type variable to ensure that it
lies in the 64-bit range supported by Long, whereas the cast in Java is handled by a
primitive bytecode cast instruction. However, even in Java, extraneous casts clearly hurt
performance.
To solve this problem, we designed and implemented the IntegerOkay analysis that identifies
variables that can be safely declared to be of Long type, thus eliminating the need for costly
typecasting on these variables.
8.2 Effect on Performance
To understand the effect on performance caused by typecasting consider a simple example of X10
code shown in listing 8.1 that just loops over a 2-dimensional array and sets each element
A(i,j) to A(i-1,j-1) + A(i+1, j+1). In this example, the index variables i and j are
declared to be of type Double and are typecast to Long when used for indexing into the array.
This example reflects the type of X10 code that we would generate if we do not have the
IntegerOkay analysis.
Listing 8.2 shows the same example, but with i and j declared to be Long, and thus not
requiring an explicit typecast. This example reflects the code that we would be able to generate
with a good IntegerOkay analysis.
static def useDoubles(scale:Double, n:Long){ val a: Array_2[Double] = new Array_2[Double](Mix10.rand(scale, scale)); var i:Double = 0; var j:Double = 0; var v:Long = 0; for (v=0;v<n;v++){ for (j=1;j<a.numElems_2-1;j++){ for (i=1;i<a.numElems_1-1;i++){ a(i as Long,j as Long) = a(i as Long -1, j as Long -1) + a(i as Long +1, j as Long +1); } } } }
Listing 8.1:
Example
for
using
Double
variables
for
array
indexing
static def useLongs(scale:Double, n:Long){ val a: Array_2[Double] = new Array_2[Double](Mix10.rand(scale, scale)); var i:Long = 0; var j:Long = 0; var v:Long = 0; for (v=0;v<n;v++){ for (j=1;j<a.numElems_2-1;j++){ for (i=1;i<a.numElems_1-1;i++){ a(i, j) = a(i-1, j-1) + a(i+1, j+1); } } } }
Listing 8.2:
Example
for
using
Long
variables
for
indexing
|
|
|
|
|
| | input args: 100, 200000 | input args : 10000, 20
|
|
|
|
|
|
| | Java | C++ | Java | C++ |
|
|
|
|
|
| useDoubles | 6.9 | 33.7 | 7.6 | 35.2 |
| useLongs | 3.4 | 1.5 | 3.7 | 2.0 |
|
|
|
|
|
| |
Table 8.1: Running times (in seconds) for listings 8.1 and 8.2, smaller is better
Table 8.1 shows running times (in seconds) for these two examples for different values of
input arguments. For the listing 8.1, the C++ code generated by the X10 compiler is nearly 5
times slower as compared to the Java code generated from X10 for the same example. Compared
to 8.2 it is slower than the C++ code for this example by almost 20 times. On the other hand, Java
code for the listing 8.1 is nearly 2 times slower compared to the Java code for the listing 8.2. For
the C++ backend, since the C++ compiler does not provide the checks for Double to
Long typecast, it is implemented in the X10 C++ backend. For the Java backend,
X10 relies on these checks provided by the JVM. The more efficient implementation
of these checks in the JVM, compared to that in the X10 C++ backend explains for
comparatively lower slowdowns for the Java code. Section 9.7 gives detailed evaluation of
the performance benefits obtained by using IntegerOkay analysis on our benchmark
set.
8.3 An Overview of the IntegerOkay Analysis
In this section we give a high-level overview of how the IntegerOkay analysis works. A detailed
algorithm for it is provided in the next section (section 8.4). The basic idea behind the
IntegerOkay analysis is that, for each variable x, if for every use and every definition of x in the
given MATLAB function, x can be safely assumed to be an integer, i.e. its declaration as an integer
does not change the result of the program, then it can be declared as an integer. Thus, the problem
boils down to answering the question of whether each use or a definition, x can be safely assumed
to be an integer.
There are three possible answers to this question:
- IntegerOkay: The variable use/def can be safely assumed to be an integer. For
example, for a definition like x = 2.0 or for use as an array index like A(x), it is
safe to assume that if x was declared to be an integer, this definition or use will not
affect the result of the program. In other words, for this definition or use of x, x is
IntegerOkay.
- Not IntegerOkay: The variable cannot be an integer type. For example consider the
expression x/y. Here, since the type of the operands can affect the result of the
division operation, it is unsafe to assume that x and y can be of integer type for this
particular use. As another example, consider the definition x = 3.14. Here, since
assuming x to be an integer will result in an error, x is not IntegerOkay.
- Conditionally IntegerOkay: It is possible to have a case where a variable x, for a
particular use or def in the function, is an integer only if some other variable, say
y, is IntegerOkay everywhere in the given function. In such a case, we say that x is
conditionally IntegerOkay and depends on y. For example, in a definition like x =
a+b, x can be an integer if both a and b can be integers everywhere in the function.
We say x is conditionally IntegerOkay and depends on a and b. Note that these
particular uses of a and b are IntegerOkay because the plus() builtin can be used
with integers safely. However, some other statement may constrain the solution. For
example, a definition of the form a = 3.2 somewhere in the function would mean
that a is not IntegerOkay everywhere and thus x is not IntegerOkay.
In our MIX10 compiler we solve the IntegerOkay problem using a simple fixed-point
computation. For each variable use and definition, the algorithm initially associates it with one of
the three abstract values above. We then compute the fixed-point by iteratively refining the
dependency lists of the conditional variables. Consider each variable x, if every use and definition
of x has been determined to be IntegerOkay, then x is removed from the dependency lists of all the
variables that are Conditionally IntegerOkay and depend on x. Once the dependency list for a
particular use or definition of a variable is empty, it is upgraded to be IntegerOkay for that
particular use or definition.
If a variable is not IntegerOkay at some point in the function or its dependency list does not
become empty for some point in the function (say, for circular dependency), it cannot
be declared as an integer. Since, every time we declare a variable to be integer, one
or more Conditionally IntegerOkay variables might be upgraded to IntegerOkay, we
iteratively repeat the process of finding variables that are IntegerOkay at all points in the
function, until we reach a fixed point. Note that since we never downgrade a variable to
Not IntegerOkay or Conditionally IntegerOkay, our iterative algorithm will always
terminate.
8.4 The Analysis Algorithm
The IntegerOkay analysis is an intra-procedural, flow-insensitive and path-insensitive analysis.
The basic idea behind identifying whether a variable can be declared as an integer is that if a
variable can safely be an integer for its every definition and every use in the function, independent
of any other variable’s type, then it can be declared to be an integer for the entire function. It is
important that any variable identified as IntegerOkay must be safe to be declared as an
integer, thus the analysis takes a conservative approach and identifies a variable as
IntegerOkay only when it is completely unambiguous. This eliminates any false-positives (a
variable is identified as IntegerOkay, when in fact it is not IntegerOkay) but
may lead to some false-negatives (a variable is identified not IntegerOkay, when in
fact it could be intgerOkay). For example, if a variable i is used as an array index
variable and also used as an argument to the rdivide() builtin call somewhere in
the function, the analysis identifies it as not IntegerOkay, even though under the
assumption that the function would execute without any runtime errors, i would be
IntegerOkay (use of a non-integral value as an array index results in a runtime
error).
The input to the analysis is a set of all the double variables in the function, a set of definitions
for each of the variables in this set, and a set of all the uses for each of the variables in
this variable set. The aim is to output a set of variables that can be safely declared as
integers.
8.4.1 STEP 1 : Initialization
As mentioned in Sec. 8.3, the analysis initializes each definition and each use of every variable to
one of the three abstract values and assigns a set of dependency variables if the assigned abstract
value is conditionally IntegerOkay.
The analysis represents these three abstract values by the following state values : IntOk,
NotIntOk, and CondIntOk for is IntegerOkay, not IntegerOkay, and conditionally
IntegerOkay respectively. Furthermore, let d.state be the state of variable v for definition d , and
u.state be the state of variable v for use u. Also, let d.deps be a set of variables on which the
CondIntOk state for variable v for definition d depends on. Similarly, let u.deps be a set of
variables on which the CondIntOk state for variable v for use u depends on. The analysis starts
with a set of all the double variables V in the MATLAB function, where each variable v has an
associated set of its definitions D and uses U. Every d.state and u.state is initialized to
NotIntOk and every d.deps and u.deps is initially set to ∅. Algorithm 1 gives the algorithm for
the initialization step of the analysis. It checks for every definition and every use of
each variable and assocites an IntegerOkay state with each use and definition. It also
assocites a dependency list of variables whose state affects the state of the variable in
question.
38:  Let u.deps be the dependency list of variable v for use u 39: for all v ∈ V do 40: for all d ∈ v.D do 41: d.deps ← d.deps-v′ 42: if d.deps = ∅ then 43: d.state ←IntOk 44: end if 45: end for 46: for all u ∈ v.U do 47: u.deps ← u.deps-v′ 48: if u.deps = ∅ then 49: u.state ←IntOk 50: end if 51: end for 52: end for 53: end procedure
Let u.deps be the dependency list of variable v for use u 39: for all v ∈ V do 40: for all d ∈ v.D do 41: d.deps ← d.deps-v′ 42: if d.deps = ∅ then 43: d.state ←IntOk 44: end if 45: end for 46: for all u ∈ v.U do 47: u.deps ← u.deps-v′ 48: if u.deps = ∅ then 49: u.state ←IntOk 50: end if 51: end for 52: end for 53: end procedure
8.4.2 STEP 2: The Fixed Point Solver
Once the initial state has been assigned for each use and each definition of every variable in STEP
1, the next step is to find the variables that can be of integer type across the function. The fixed
point solver iteratively finds these variables until a fixed point is reached and no more variables
are safe to be defined as integers.
The input to the fixed point solver is the set of all double variables V with state
and dependency list initialized for each definition and each use of every variable v in
V . The output of the fixed point solver is V′, the set of variables that can be safely
defined as integers. The fixed point solver also defines the variable v.State that stores the
final state value for the variable v in the function, independent of any use or definition.
For each variable v, v.State is assigned an initial empty value ~. V′ is initially set to
∅.
Algorithm 2 provides an algorithm for this fixed point solver. Note that the algorithm uses a
 operator to merge the state values of various definitions and uses of a variable to obtain its
final state. Table 8.2 gives a definition of the
operator to merge the state values of various definitions and uses of a variable to obtain its
final state. Table 8.2 gives a definition of the  operator used by this analysis. In the
table, CondIntOk(s,s = ∅) is the case when d.deps∪u.deps = ∅ for a variable v, and
CondIntOk(s,s≠∅) is the case when d.deps∪u.deps≠∅.
operator used by this analysis. In the
table, CondIntOk(s,s = ∅) is the case when d.deps∪u.deps = ∅ for a variable v, and
CondIntOk(s,s≠∅) is the case when d.deps∪u.deps≠∅.
|
|
|
|
|
|
 | IntOk | CondIntOk(s,s = ∅) | CondIntOk(s,s≠∅) | NotIntOk | ~ |
|
|
|
|
|
|
|
|
|
|
|
|
| IntOk | IntOk | IntOk | NotIntOk | NotIntOk | IntOk |
|
|
|
|
|
|
| CondIntOk(s,s = ∅) | IntOk | IntOk | NotIntOk | NotIntOk | CondIntOk(s,s = ∅) |
|
|
|
|
|
|
| CondIntOk(s,s≠∅) | NotIntOk | NotIntOk | NotIntOk | NotIntOk | CondIntOk(s,s≠∅) |
|
|
|
|
|
|
| NotIntOk | NotIntOk | NotIntOk | NotIntOk | NotIntOk | NotIntOk |
|
|
|
|
|
|
| ~ | IntOk | CondIntOk(s,s = ∅) | CondIntOk(s,s≠ ∅) | NotIntOk | ~ |
|
|
|
|
|
|
| |
Table 8.2: Definition of the  merge operator
merge operator
8.5 An Example
Consider the following pseudocode for example:
/*1*/ x = 3.0;
/*2*/ y = 3.14;
/*3*/ z = x+y;
/*4*/ for (i = 0; i < 5; i++)
/*5*/ y = y+i;
/*6*/ end
In this example, the initialization step proceeds as follows. On line 1, x is IntegerOkay since 3.0 is
a real integer. On line 2, y is Not IntegerOkay. On line 3, z is Conditionally IntegerOkay and
depends on x and y, whereas x and y are IntegerOkay in their use in the expression x+y. On line
4, i is IntegerOkay in its definition i = 0, in its use in the expression i < 5, and also in
the definition i++. On line 5, y is conditionally IntegerOkay and depends on i in its
definition and it is IntegerOkay in its use in y+i. i is IntegerOkay in its use in y+i. Note
that on line 5, we do not include y in its own dependency list, since if we say, y is
conditionally IntegerOkay and depends on y, it is safe to declare y as integer as long as
it does not have any other dependencies and is IntegerOkay everywhere else in the
function.
The fixed-point solver for this example proceeds as follows. We look for variables that are
IntegerOkay at every point in the function. x and i are two such variables and we can
declare them to be an integer. We also remove x from the dependency list of definition
of z on line 3, and i from the dependency list of definition of y on line 5. Next, we
search again and find that y is IntegerOkay in its use on line 3 and line 5, and also in
its definition on line 5, however it is Not IntegerOkay in its definition on line 2 and
thus it cannot be declared as an integer. z on line 3 is dependent on y and thus it can
also not be declared as an integer. At this point, we have reached a fixed point since
there are no more upgrades. Finally, we declare x and i as integers, and y and z as
doubles.
Chapter 9
Evaluation
___________________________________________________________________________________
In this chapter we evaluate the performance of our compiler. In this research our main aim was
to generate X10 code for MATLAB such that its sequential performance would be comparable to
the performance provided by the state of the art tools which translate MATLAB to more traditional
imperative languages such as C and Fortran. To demonstrate our results, we compiled a set of 17
MATLAB programs to X10 via the MIX10 compiler and compared their performance
results with those of the original MATLAB programs, C programs generated for our
benchmarks via the MATLAB coder, and Fortran programs generated by the MC2FOR
compiler.We also compared our results to Octave, a widely used open source alternative to MATLAB. However, since
Octave involves an interpreter, it performed slower than the standard MATLAB compiler (with a mean slowdown of
66.67 times slower) over all of our benchmarks, thus in this section we do not concentrate on comparison of our
results with Octave.
In addition to showing our best overall sequential performance, we also demonstrate the
results of compiling the generated X10 code to Java compared to C++, effects on the
performance for the various efficiency enhancing techniques discussed in this thesis, and
finally the performance of the parallel X10 code generated for MATLAB parfor
loops.
9.1 Benchmarks
The set of benchmarks used for our experiments consists of benchmarks from various sources; Most of
them are from related projects like FALCON [RP99] and OTTER [QMSZ98a], Chalmers university of
Technologyhttp://www.elmagn.chalmers.se/courses/CEM/ , “Mathworks’
central file excahange”http://www.mathworks.com/matlabcentral/fileexchange ,
and the presentation on parallel programming in MATLAB by Burkardt and
Cliff .
This set of benchmarks covers the commonly used MATLAB features like arrays of
different dimensions, loops, use of numerical functions like random number generation,
trigonometric operations, and array operations like transpose and matrix multiplication.
Table 9.1 gives a description of all the benchmarks we used and shows their special
features.
|
|
|
|
| Benchmark | Source | Description | Key features |
|
|
|
|
| bbai | MATLAB file exchange | Implementation of the Babai
estimation algorithm | 2-D arrays, random number
generation |
| bubl | McLab | Bubble sort | 1-D array, nested loops |
| capr | Chalmers University | Computes the capacitance of a
transmission line using
finite difference and Gauss-Seidel
method | Array operations on 2-D arrays,
nested loops |
| clos | Otter project | Calculates the transitive closure of
a directed graph | Matrix multiplication, 2-D arrays |
| crni | Falcon project | Crank-Nicholson solution to the
heat equation | read/write operations on a very
large 2-D array |
| dich | Falcon project | Dirichlet solution to Laplace’s
equation | Array operations on 2-D arrays,
nested loops |
| diff | MATLAB file exchange | Calculates the diffraction pattern of
monochromatic light | 2-D arrays, Concatenation
operations, complex numbers |
| edit | MATLAB file exchange | Calculates the edit distance
between two strings | many 1-D arrays of characters |
| fiff | Falcon project | Computes the finite difference
solution to the wave equation | Array operations on 2-D arrays,
nested loops |
| lgdr | | Calculates derivatives of Legendre
polynomials | Array transpose on row vectors |
| mbrt | MCFOR project | Computes Mandelbrot sets | Complex numbers, parfor loop |
| nb1d | Otter project | Simulates the 1-dimensional
n-body problem | Column-vectors, nested loops,
parfor loop |
| matmul | McLab | naive matrix multiplication | 2-D arrays, nested loops, parfor
loop |
| mcpi | McLab | Calculates π by the Monte Carlo
method | Scalar values, Random number
generation, parfor loop |
| numprime | Burkardt and Cliff | Simulates the sieve of Eratosthenes
for calculating number of prime
numbers less than a given number | Scalar values, nested loops,
parfor loop |
| optstop | Burkardt and Cliff | Solution to the optimal stopping
problem | Row vectors, random number
generation, parfor loop |
| quadrature | Burkardt and Cliff | Simulates the quadrature approach
for calculating integral of a function | Scalar values, parfor loop |
|
|
|
|
| |
Table 9.1: Benchmarks
9.2 Experimental Setup
We used Mathworks’ MATLAB release R2013a to execute our benchmarks in MATLAB and
MATLAB coder. We also executed them using the GNU Octave version 3.2.4. We compiled our
benchmarks to Fortran using the MC2FOR compiler and compiled the generated Fortran code
using the GCC 4.6.3 GFortran compiler with optimization level -O3. To compile the generated
X10 code from our MIX10 compiler, we used X10 version 2.4.0. We used OpenJDK Java
1.7.0_51 to compile and run Java code generated by the X10 compiler, and GCC 4.6.4 g++
compiler to compile the C++ code generated by the X10 compiler. All the experiments were run
on a machine with Intel(R) Core(TM) i7-3820 CPU @ 3.60GHz processor and 16 GB memory
running GNU/Linux(3.8.0-35-generic #52-Ubuntu). For each benchmark, we used an input
size to make the program run for approximately 20 seconds on the de facto MATLAB
compiler. We used the same input sizes for compiling and running benchmarks via
other compilers. We collected the execution times (averaged over five runs) for each
benchmark and compared their speedups over Mathworks’ MATLAB runtimes (normalized to
one).
9.3 X10 Compiler Variations
The MIX10 compiler compiles the source MATLAB code to X10 code, which is then compiled
by the X10 compiler. The X10 compiler is also a source to source compiler that provides two
backends, a C++ backend that generates C++ code and a Java backend that generates Java code,
which are then compiled by their respective compilers to executable code. Both these backends
provide a -NO_CHECKS switch that generates the C++/Java code that does not include dynamic
array bounds checks, which are otherwise included by default. As we described in section 4.1.1,
we altered the X10 compiler to use column-major array indexing. We always used the -O
optimization flag for the X10 compiler for both the backends, with notable exceptions
where the X10 optimizer generated code which interacted extremely negatively with
the Java JIT, as discussed in section 9.5.1. For all of our experiments, we used our
IntegerOkay analysis, except for the experiment which investigates the performance impact of
this analysis. Our best results were obtained by compiling the generated X10 code
with the C++ backend with -NO_CHECKS enabled, where the X10 code itself was
generated by the MIX10 compiler with simple arrays and our IntegerOkay analysis
enabled.
9.4 Overall MIX10 Performance
We compared the performance of the generated X10 code with that of the original MATLAB code
run on Mathworks’ implementation of MATLAB. To compare against the state of the art static
compilers, we also compared the performance of the MIX10 generated X10 code with the C
code generated by MATLAB coder and the Fortran code generated by the MC2FOR
compiler.

Figure 9.1: Performance of MIX10 vs other state-of-the-art static compilers, reported as
speedups relative to Mathworks’ MATLAB, higher is better.
Figure 9.1 shows the speedups and slowdowns for the code generated for our benchmarks by
different compilers. For MIX10 we have included the results for the X10 code compiled by the
X10 C++ backend compiled, once with -NO_CHECKS enabled and once with -NO_CHEKCS
disabled. For Fortran we included the results for the code generated without bounds checks. C
code from MATLAB coder was generated with default settings and includes bounds checks. We
also calculated the geometric mean of speedups(slowdowns) for all the benchmarks for each
compiler.
Overall, one can see that the static compilers all provide excellent speedups, often of at least
an order of magnitude faster. Thus, for the kinds of benchmarks in our benchmark set, it would
seem that tools like the MATLAB coder, MC2FOR, and our MIX10 tools are very useful. MIX10
outperforms MATLAB coder in 9 out of 17 benchmarks, when compared with the X10 version
compiled with bounds checks, and 10 out of 17 benchmarks when compared with the
version with no bounds checks. For Fortran, the generated X10 does better in 7 out
of 17 benchmarks with no bounds checks, and 6 out of 17 benchmarks with bounds
checks enabled. Note that MATLAB coder was not able to compile 1 of our benchmarks
(diff ) due to the dynamic array growth involved in it; MIX10 supports dynamic array
growth.
We achieved a mean speedup of 4.8 over MATLAB, for the X10 code with bounds checks,
and 6.8 for the x10 code with no bounds checks. On the other hand, MATLAB coder
gave a mean speedup of 6.3 and MC2FOR gave a mean speedup of 10.2. However, we
noticed that our mean result was skewed due to two benchmarks for which the generated
X10 performed very poorly compared to the generated C code. These benchmarks
are clos and lgdr. In the following paragraphs we explain the reason for their poor
performance. If we do not consider these two benchmarks, we get a mean speedup of 6.7 for
the X10 code with bounds checks compared to 5.2 for the C code. For the X10 code
compiled with no bounds checks we get a mean speedup of 9.3 compared to 11.6 for
Fortran.
clos involves repeated calls to the builtin matrix multiplication operation for the 2-dimensional
matrices. The generated C code from MATLAB coder uses highly optimized matrix multiplication
libraries compared to the naive matrix multiplication implementation used by MIX10. Thus,
MIX10 gets a speedup of 0.02 as compared to 1.05 for C. Note that the generated Fortran code is
also slowed down (speedup of 0.04) due to the same reason. As a future work, We plan to
replace our matrix multiplication implementation with calls to an optimized library
function.
lgdr involves repeated transpose of a row vector to a column vector. MATLAB and Fortran,
both being array languages are highly optimized for transpose operations. MIX10 currently uses a
naive transpose algorithm which is not optimized. We did achieve a speedup of over 10 times
compared to MATLAB but it is not as good as the speedups achieved by C (speedup of 505.0) and
Fortran (speedup of 336.7). For transpose operation also, we plan to replace our current
implementation with an optimized implementation or a call to an optimized library
function.
Both of these examples show that in addition to generating good code, another important task
is developing optimized X10 library routines for key array computations.
Other interesting numbers are shown by optstop, fiff, nb1d, and quadrature. optstop
gave a speedup of just 1.5 even without bounds checks. It involves repeated random
number generation, which our experiments showed to be slow for the X10 C++ backend
compared to Fortran and even the Java backend. This problem is worse with C, due to
which the C code from MATLAB coder gives a speedup of mere 0.6(slowdown). Fortran
performs better with a speedup of 4.3. bbai shows a similar pattern due to the same
reason.
fiff is characterized by stencil operations in a loop on a 2-dimensional array. These
operations are also optimized by array-based languages like Fortran and MATLAB. For
nb1d, Fortran performs better due to the use of column vectors in the benchmark, which
are represented as 2-dimensional arrays in X10 but in Fortran they are represented as
1-dimensional and are optimized. 2-dimensional arrays are not as fast in X10 as the
1-dimensional arrays. quadrature involves repeated arithmetic calculations on a range of
numbers. We achieve a speedup of about 200 times compared to MATLAB, however it is
slow compared to speedups of 3348 and 502 by C and Fortran respectively. We believe
that MATLAB coder leverages partial evaluation for optimizing numerical methods’
implementations.
For most of the other benchmarks, we perform better or nearly equal to C and Fortran code.
Despite the facts that: (1) the sequential core of X10 is a high-level object oriented language
which is not specialized for array-based operations; and (2) Generating the executable binaries via
MIX10 involves two levels of source-to-source compilations (MATLAB → X10 →
C++); we have achieved performance comparable to C, the state of the art in statically
compiled languages and Fortran, a statically compiled language highly specialized for
arrays.
9.5 X10 C++ Backend vs. X10 Java Backend
The X10 compiler provides two backends, a C++ backend that compiles the X10 code to native
binary via C++, and a Java backend that compiles the X10 code to JVM code via Java.
We were interested to see how well these backends perform when used to compile
the MIX10 generated code. Even though we did not expect Java code to perform as
well as the C++ code, our aim was to make sure that we achieved good performance,
significantly better than MATLAB, for the X10 Java backend. This would enable MATLAB
programmers to use our MIX10 compiler to generate code that could be integrated into Java
applications.
In this section we present the performance comparison of the MIX10 generated X10 code
compiled by the X10 C++ backend with that compiled by the X10 Java backend. Columns 3 and
4 of the Table 9.2 show speedups for our benchmarks compiled with the X10 C++ backend
without bounds checks, and with bounds checks respectively. Columns 5 and 6 show these values
for compilation with the X10 Java backend without bounds checks, and with bounds
checks respectively. We also show the geometric mean of the speedups for all the 4
cases.
|
|
|
|
|
|
| Benchmark | Matlab | C++ (no checks) | C++ (checks) | Java (no checks) | Java (checks) |
|
|
|
|
|
|
| bbai | 1 | 4.9 | 4.9 | 11.3 | 10.7 |
| bubl | 1 | 15.8 | 10.8 | 7.5 | 7.5 |
| capr | 1 | 13.5 | 12.7 | 11.1 | 6.3 |
| clos | 1 | 0.03 | 0.02 | 0.02 | 0.002 |
| crni | 1 | 6.5 | 5.3 | 5.6 | 4 |
| dich | 1 | 7.6 | 7.3 | 7 | 1.6 |
| diff | 1 | 4.6 | 4.4 | 0.3 | 0.3 |
| edit | 1 | 29.7 | 19.4 | 22.1 | 20 |
| fiff | 1 | 9.8 | 3.5 | 2.1 | 1.4 |
| lgdr | 1 | 13.5 | 11.9 | 10.6 | 10.6 |
| mbrt | 1 | 6.5 | 6.5 | 0.3 | 0.3 |
| nb1d | 1 | 6.2 | 4.8 | 5.5 | 4.1 |
| matmul | 1 | 14.7 | 2.5 | 1.1 | 0.8 |
| mcpi | 1 | 3.3 | 2.5 | 2.9 | 3 |
| numprime | 1 | 7.6 | 6.8 | 6.5 | 6.4 |
| optstop | 1 | 1.5 | 1.2 | 1.8 | 1.4 |
| quadrature | 1 | 200.9 | 182.6 | 167.4 | 154.5 |
|
|
|
|
|
|
| Geometric mean | 1 | 6.8 | 4.8 | 3.4 | 2.4 |
|
|
|
|
|
|
| |
Table 9.2: MIX10 performance comparison : X10 C++ backend vs. X10 Java backend,
speedups relative to Mathworks’ MATLAB, higher is better
The mean speedups for the C++ backend are 6.8 and 4.8 respectively for the version with
bounds checks switched off, and the version with bounds checks switched on, whereas for Java
backend these values are 3.4 and 2.4 respectively. This is expected, given that C++ is compiled to
native binary while Java is JIT compiled.
bbai and optstop are the two exceptions, where Java performs better than C++. For bbai, both
the Java versions gave a speedup of over 10, whereas for C++, the speedup is under 5 for both the
versions. For optstop, the difference is not large, with C++ speedup at 1.5 (1.2 for the bounds
checks version) compared to 1.8 (1.4 for the bounds checks version) for the Java backend.
bbai is slower with X10 C++ backend because it includes repeated calls to the X10’s
Random.nextDouble() function to generate random numbers. We found it to be
significantly slower in the C++ backend compared to the Java backend. We have reported our
findings to the X10 development team and they have validated our findings. optstop
is slower for the same reason : It also involves repeated random number generation.
Note that for these two benchmarks, even the C code generated via MATLAB coder
is slower than the C++ code, with speedups of 4.2 and 0.6 respectively for bbai and
optstop.
Other interesting results are for the benchmarks diff, fiff, mbrt and matmul. For these
benchmarks, results from the Java backend are significantly slower compared to the C++ backend.
diff and mbrt involve operations on complex numbers. In the X10 C++ backend, complex
numbers are stored as structs and are kept on the stack, whereas in the Java backend, they are
stored as objects and reside in the heap storage. fiff and matmul are characterized by repeated
array access and read/write operations on 2-dimensional arrays. For these benchmarks, the
Java backend performs significantly slower compared to the C++ backend with no
bounds checks(2.1 vs. 9.8 for fiff and 1.1 vs. 14.7 for matmul), however compared to the
performance by the C++ beckend with bounds checks, it is not as slow(2.1 vs. 3.5 for
fiff and 1.1 vs. 2.5 for matmul). The reason is that even with bounds checks turned
off for the X10 to Java compiler, The Java compiler by default has bounds checks
on. These checks have a significant effect on performance for 2-dimensional array
operations.
9.5.1 When Not to Use the X10 -O
One of the most surprising results in this set of experiments was the fact that we had to sometimes
disable the X10 -O optimizer switch when using the X10 Java backend.. For the benchmarks
capr and dich, in the case when X10 bounds checks are switched on, we found very pathological
performance, with slowdowns of over 2 orders of magntitude, when the X10 compiler’s
optimization switch(-O) was used.
We recorded running times of 785.3 seconds for capr compared to 3.2 seconds without the
optimization, and 1558.9 seconds for dich compared to 12.7 seconds without the optimization.
With the help of the X10 development team we determined that switching on the optimization
triggered code inlining for the array bounds check code, which then caused the resultant Java
program to be too large to be handled by the JIT compiler. In fact, the Java JIT effectively gives
up on this code and reverts to the interpreter.
Thus, it would seem that the X10 optimizer needs to be improved in order to apply aggressive
inlining only when it does not have a negative impact on code size, and that different inlining
strategies are needed for the C++ and Java backends.
9.6 Simple vs. Region Arrays
One of the key optimizations used by MIX10 is to use simple arrays, wherever possible, for
higher performance. In this section we discuss the performance gains obtained by using simple
arrays over region arrays and the specialized region arrays. A description of these three kinds of
arrays provided by X10 was given in Sec. 2.1.3. Table 9.3 shows the relative speedups and
slowdowns for our benchmarks compiled to use different kinds of X10 arrays for the C++
backend and the Java backend.
|
|
|
|
|
|
|
|
| | | X10 C++ backend | X10 Java backend |
|
|
|
|
|
|
|
|
| Benchmark | Matlab | Simple arrays | Region arrays | Sp. region arrays | Simple arrays | Region arrays | Sp. region arrays |
|
|
|
|
|
|
|
|
| bbai | 1.0 | 4.9 | 2.7 | 2.7 | 11.3 | 6.4 | 6.6 |
| bubl | 1.0 | 15.8 | 11.4 | 11.6 | 7.5 | 3.6 | 3.7 |
| capr | 1.0 | 13.5 | 11.6 | 12.4 | 11.1 | 0.02 | 10.5 |
| clos | 1.0 | 0.03 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 |
| crni | 1.0 | 6.5 | 3.6 | 3.9 | 5.6 | 4 | 4.1 |
| dich | 1.0 | 7.6 | 6.7 | 7.0 | 7.0 | 0.01 | 0.02 |
| diff | 1.0 | 4.6 | 4.2 | 4.3 | 0.3 | 0.3 | 0.3 |
| edit | 1.0 | 29.7 | 4.3 | 3.6 | 22.1 | 9.4 | 9.4 |
| fiff | 1.0 | 9.8 | 2.0 | 2.8 | 2.1 | 1.4 | 1.4 |
| lgdr | 1.0 | 13.5 | 1.6 | 1.5 | 10.6 | 5.4 | 5.4 |
| mbrt | 1.0 | 6.5 | 6.3 | 6.5 | 0.3 | 5.1 | 5.1 |
| nb1d | 1.0 | 6.2 | 0.3 | 0.3 | 5.5 | 1.4 | 1.4 |
| matmul | 1.0 | 14.7 | 1.3 | 1.4 | 1.1 | 0.5 | 0.5 |
| mcpi | 1.0 | 3.3 | 2.8 | 2.7 | 2.9 | 3.0 | 3.0 |
| numprime | 1.0 | 7.6 | 5.7 | 5.7 | 6.5 | 6.3 | 6.3 |
| optstop | 1.0 | 1.5 | 0.4 | 0.4 | 1.8 | 1.2 | 1.3 |
| quadrature | 1.0 | 200.9 | 200.9 | 200.9 | 167.4 | 143.5 | 154.5 |
|
|
|
|
|
|
|
|
| Geometric mean | 1.0 | 6.8 | 2.7 | 2.8 | 3.4 | 1.3 | 1.9 |
|
|
|
|
|
|
|
|
| |
Table 9.3: MIX10 performance comparison : Simple arrays vs. Region arrays vs.
Specialized region arrays, speedup relative to Mathworks’ MATLAB, higher is better
For the C++ backend we obtained a mean speedup of 6.8 for Simple arrays, compared to 2.7
for region arrays and 2.8 for specialized region arrays. For the Java backend, we obtained
speedups of 3.4, 1.3 and 1.9 for the simple arrays, region arrays, and the specialized region arrays
respectively. These results are as expected in Sec. 4.1. For the C++ backend, most noticeable
performance differences between simple arrays and region arrays are for edit, fiff, lgdr, nb1d,
matmul and optstop. All of these benchmarks are characterized by large number of array accesses
and read/write operations on 2-dimensional arrays, except optstop and edit, which have multiple
large 1-dimensional arrays. The performance difference is most noticeable for nb1d, where the
region arrays are about 20 times slower than the simple arrays. This is because nb1d involves
simple operations on a large column vector. With simple arrays, since the compiler
knows that it is a column vector, rather than a 2-dimensional matrix, even though it is
declared as a 2-dimensional array, the performance can be optimized to match that of
the underlying Rail. However, this is not possible for region arrays where the size
of each dimension is not known statically. For the C++ backend, we do not observe
significant performance differences between the region arrays and the specialized region
arrays.
For the Java backend we observed a higher difference in the mean performance for the simple
arrays and the region arrays. The mean speedup for region arrays is 1.3 whereas for simple
arrays it is nearly 3 times more at 3.4. There is also a significant difference between the
performance of specialized region arrays and region arrays. Speedup for specialized
region arrays is 1.9. Like the C++ backend, here also, most noticeable performance gain
for simple arrays is for benchmarks involving a large number of array accesses and
read/writes. capr and dich ask for special consideration. For capr, even with X10 compiler’s
bounds checks turned off, the region array version slows down by more than 500 times
compared to the simple array version and even the specialized region array version. This
again, is due to the fact that region arrays, with the dynamic shape checks, generated
more code than the JIT compiler could handle. For dich the slowdown due to region
arrays was about 700 times compared to simple arrays. For dich, even the specialization
on region arrays was not enough to reduce the code size enough to be able to be JIT
compiled.
9.7 Effect of the IntegerOkay Analysis
In this section we present an overview of the performance improvements achieved by MIX10 by
using the IntegerOkay analysis. Table 9.4 shows a comparison of speedups gained by using the
IntegerOkay analysis over those without using it. For this experiment we used results with X10
optimizations turned on and bounds checks turned off.
|
|
|
|
|
|
| | | X10 C++ backend | X10 Java backend |
|
|
|
|
|
|
| Benchmark | Matlab | IntegerOkay | All Doubles | IntegerOkay | All Doubles |
|
|
|
|
|
|
| bbai | 1.0 | 4.9 | 3.8 | 11.3 | 8.2 |
| bubl | 1.0 | 15.8 | 2.2 | 7.5 | 4.2 |
| capr | 1.0 | 13.5 | 1.7 | 11.1 | 9.7 |
| clos | 1.0 | 0.03 | 0.02 | 0.02 | 0.01 |
| crni | 1.0 | 6.5 | 2.8 | 5.6 | 5.5 |
| dich | 1.0 | 7.6 | 1.0 | 7.0 | 5.8 |
| diff | 1.0 | 4.6 | 4.5 | 0.3 | 0.3 |
| edit | 1.0 | 29.7 | 13.5 | 22.1 | 20.0 |
| fiff | 1.0 | 9.8 | 1.0 | 2.1 | 1.8 |
| lgdr | 1.0 | 13.5 | 10.1 | 10.6 | 11.0 |
| mbrt | 1.0 | 6.5 | 6.1 | 0.3 | 0.3 |
| nb1d | 1.0 | 6.2 | 5.2 | 5.5 | 5.5 |
| matmul | 1.0 | 14.7 | 14.5 | 1.1 | 1.2 |
| mcpi | 1.0 | 3.3 | 3.3 | 2.9 | 2.9 |
| numprime | 1.0 | 7.6 | 7.6 | 6.5 | 7.1 |
| optstop | 1.0 | 1.5 | 1.0 | 1.8 | 1.0 |
| quadrature | 1.0 | 200.9 | 182.6 | 167.4 | 143.5 |
|
|
|
|
|
|
| Geometric mean | 1.0 | 6.8 | 3.4 | 3.4 | 2.9 |
|
|
|
|
|
|
| |
Table 9.4: Performance evaluation for the IntegerOkay analysis, speedups relative to
Mathworks’ MATLAB, higher is better
For the C++ backend, we observed a mean speedup of 6.8 which is two times the speedup
gained by not using the IntegerOkay analysis, which is equal to 3.4. We observed a significant
gain in performance by using IntegerOkay analysis for the benchmarks that involve significant
number of array indexing operations. bubl, capr, crni, dich, and fiff show the most
significant performance gains. The reason for this behaviour is that, X10 requires all array
indices to be of type Long, thus if the variables used as array indices are declared to be
of type Double (which is the default in MATLAB), they must be typecast to Long
type. Double to Long is very time consuming because every cast involves a check
on the value of the Double type variable to ensure that it can safely fit into Long
type.
For the Java backend, with the IntegerOkay analysis, we get a mean speedup of 3.4 as
compared to 2.9 without it. The reason for the lower difference as compared to that for the C++
backend is that, for Java backend, the X10 compiler does not generate the value checks for
Double type values, instead it relies on the JVM to make these checks, resulting in a better
performance. Also note that, without the IntegerOkay analysis, the C++ backend results are
slower than the Java backend results for 9 out of 17 benchmarks.
To conclude, IntegerOkay analysis is very important for efficient performance of code
involving Arrays, specially for the X10 C++ backend.
9.8 MATLAB parfor vs. MIX10 Parallel Code
Given that we have established that we can generate competitive sequential code, we wanted to
also do a preliminary study to see if we could get additional benefits from the high-perfomance
nature of X10. In this section we present the preliminary results for the compilation of MATLAB
parfor construct to the parallel X10 code. 7 out of our 17 benchmarks could be safely modified
to use the parfor loop. We compare the performance of the generated parallel X10 programs
for these benchmarks to that of MATLAB code using parfor, and to their sequential X10
versions. For this experiment, we used the sequential versions of the generated X10 programs
with optimizations and no bounds checks. For the parallel versions we used both the
variants, with optimizations and bounds checks, and with optimizations and without
bounds checks. It is important to note that the Intel(R) Core(TM) i7-3820 CPU used
for this experiment has 4 CPU cores and 8 hardware threads, thus bounding the X10
parallelization speedup at 8. Table 9.5 shows the results for both the X10 C++ and the X10 Java
backends.
|
|
|
|
|
|
|
|
|
| | | | X10 C++ backend | X10 Java backend |
|
|
|
|
|
|
|
|
|
| | | | Sequential | Parallel | Sequential | Parallel
|
|
|
|
|
|
|
|
|
|
| Benchmarks | MATLAB | MATLAB parfor | No checks | No checks | Checks | No checks | No checks | Checks |
|
|
|
|
|
|
|
|
|
| mbrt | 1.0 | 1.7 | 6.5 | 25.3 | 25.3 | 0.3 | 1.3 | 1.3 |
| nb1d | 1.0 | 0.4 | 6.2 | 7.3 | 7.3 | 5.5 | 19.0 | 15.1 |
| matmul | 1.0 | 1.3 | 14.7 | 68.7 | 3.9 | 1.1 | 1.1 | 0.8 |
| mcpi | 1.0 | 4.6 | 3.3 | 15.7 | 15.9 | 2.9 | 18.1 | 18.2 |
| numprime | 1.0 | 5.3 | 7.6 | 30.0 | 30.9 | 6.5 | 24.8 | 26.4 |
| optstop | 1.0 | 4.1 | 1.4 | 2.0 | 2.1 | 1.8 | 10.7 | 9.7 |
| quadrature | 1.0 | 3.8 | 200.9 | 11.3 | 11.2 | 167.4 | 13.0 | 13.0 |
|
|
|
|
|
|
|
|
|
| Geometric mean | 1.0 | 2.3 | 8.9 | 14.5 | 9.8 | 3.7 | 7.8 | 7.1 |
|
|
|
|
|
|
|
|
|
| |
Table 9.5: Performance evaluation for MIX10 generated parallel X10 code for the
MATLAB parfor construct, speedups relative to Mathworks’ MATLAB, higher is better
For the X10 C++ backend we achieved a mean speedup of 14.5 for the generated parallel X10
code without bounds checks, which is around 7 times of the speedup for the MATLAB code with
parfor, at a speedup of 2.3. Compared to X10 sequential code which has a mean speedup of
8.9, it is more than 1.5 times as fast. Even with the parallel X10 code with bounds checks we
achieved a speedup of 9.8 which is over 4 times better than the MATLAB parfor
code. The optstop benchmark is an interesting exception. It is actually slower (at a
speedup of 2.1) than the MATLAB parfor version (at a speedup of 4.1). The sequential
version of optstop is just slightly faster than the sequential MATLAB version, with a
speedup of just 1.5 (due to the reasons explained earlier in Sec. 9.4) and the total time
for the parallel execution of each iteration, and managing the parallelization of these
activities is just slightly faster than the sequential version. We see a similar trend for the
matmul benchmark for the X10 Java backend. It shows a speedup of just 0.8 (version
with bounds checks) as compared to 1.3 for the MATLAB parfor version. For the
parallel version of matmul, the speedup for the C++ backend with checks turned on is
just 3.9 compared to 14.7 for the sequential version with no checks, however it is 1.6
times faster than the sequential version with checks, which has a speedup of just 2.5
(shown in figure 9.1). The quadrature benchmark shows very interesting numbers, with a
slowdown of about 20 times and 13 times for the parallel X10 code compared to the
sequential X10 code, for the C++ backend and the Java backend respectively. The
quadrature benchmark consists of a loop with a large number of iterations (4600000 for our
experiment), where each iteration performs an insignificant amount of computations with
just 21 simple arithmetic operations on scalar values. A sequential speedup of over
200 times compared to the sequential MATLAB code indicates the insignificance of
each iteration in terms of computation time. In the parallel X10 code, each iteration
is executed as a separate activity, and the time taken to manage the large number of
activities overshadows the sequential speedup. Also, each activity has an atomic
statement, which is a blocking construct (when one activity is executing the atomic
statement, all other activities are blocked) and adds further overhead to the activity
management system. Performance numbers for quadrature assert the fact that not all
parallel MATLAB programs are good candidates to be compiled to parallel X10 in a
straight-forward fashion, specially the ones with large number of parallel loop iterations
where each iteration itself does insignificant amount of work. As a future work, we
plan to handle such programs with more sophisticated parallelization techniques. For
example, one way to make a benchmark like quadrature more efficient would be to
break the loop into two nested loops and executing the outer loop in a parallel fashion
and the inner loop sequentially to ensure that each concurrent loop does substantial
amount of work, however the challenge here is to determine the right number of iterations
for the inner sequential loop to make it significant enough to take advantage of the
parallelization.
Overall for the Java backend, we obtained a mean speedup of 7.8 for the X10 code with no
bounds checks and 7.1 for the code with bounds checks. Compared to the MATLAB parfor version
we obtained about 3.5 times better performance. The parallel X10 code is over 2 times faster than
the sequential X10 code (speedup of 3.7). For both, the C++ backend, and the Java backend, the
mean speedup for the sequential X10 code is also substantially faster than the MATLAB parallel
code.
To conclude, the parallel X10 code provides much higher performance gains compared to the
MATLAB parfor code and even the X10 sequential code, which by itself is most of the times
faster than the MATLAB parallel code.
9.9 Summary
We showed that the MIX10 compiler with its efficient handling of array operations and
optimizations like IntegerOkay can generate X10 code that provides performance comparable to
the native code generated by the state of the art languages like C, which is fairly low-level, and
Fortran, which itself is an array-based language. As a future work, we plan to use more efficient
implementations of the builtin functions, and believe that it would further improve the
performance of the code generated by MIX10.
With MIX10, we also took first steps to compile MATLAB to parallel X10 code to take full
advantage of the high performance features of X10. Our preliminary results are very inspiring and
we plan to continue in this direction further, in the future.
In addition to demonstrating that our approach leads to good code, these experiments have
also been quite valuable for the X10 development team. Our generated code has stressed the X10
system more than the hand-written X10 benchmarks and has exposed places where further
improvements can be made.
Chapter 10
Related Work
___________________________________________________________________________________
The work in this thesis presents a research compiler for MATLAB. We provide a
source-to-source static compiler that targets the high-level, object oriented language, X10. Our
approach is open and extensible and generates sequential X10 code that is competitive in
performance to code in state-of-the-art languages like C and Fortran, generated by other MATLAB
compilers. We also generated high performance code for MATLAB’s parfor loops, that showed
great performance improvements.
10.1 Alternatives to MATLAB
Although our focus is on handling MATLAB itself, there are notable open source alternatives
of MATLAB like Scilab[INR09], Julia[BKSE12], NumPy[Sci], FreeMat[DKB] and
Octave[Oct]. Octave is an open source implementation of the MATLAB language and
supports most of the MATLAB programs, however until the recently released version 3.8.1,
Octave was solely an interpreted language and our experiments showed it to be orders of
magnitude slower than MATLAB. We would like to evaluate its performance for the latest
version that comes with a JIT compiler. Scilab and FreeMat are similar in syntax to
MATLAB but have significant differences that prevent a significant portion of MATLAB
programs to be able to run on these systems. NumPy is a python package for scientific
computing, and Julia is a technical computing language. Julia also provides a fairly
advanced distributed parallel execution environment. However, these alternative systems
concentrate on providing open library support and have not tackled the problems of static
compilation. We are investigating if there is any way of sharing some of their library
support with MIX10. A Comparative evaluation of Matlab, Octave, FreeMat, Scilab, R,
and IDL on a cluster computing system is presented in a technical report by Coman at
al. [CBP+12] The MEGHA project[PAG11] provides an interesting approach to map
MATLAB array operations to CPUs and GPUs, but supports only a very small subset of
MATLAB.
10.2 Other MATLAB Compilers
There have been previous research projects on static compilation of MATLAB which focused
particularly on the array-based subset of MATLAB and developed advanced static analyses for
determining shapes and sizes of arrays. For example, FALCON [RP99] is a MATLAB to
FORTRAN90 translator with sophisticated type inference algorithms. The McLab group has
previously implemented a prototype Fortran 95 generator [Li09], and has more recently
developed the next generation Fortran generator, MC2FOR [LH14] in parallel with the MIX10
project. Some of the solutions are shared between the projects, especially the parts which extend
the Tamer. MATLAB Coder is a commercial compiler by MathWorks[Mata], which produces C
code for a subset of MATLAB. We also compared MIX10’s performance to MATLAB coder.
Below are more details about these and few other notable MATLAB compiler research
projects:
- Falcon is a MATLAB-to-Fortran 90 compiler that applies type inference algorithms
developed for the array programming language APL [JB01, WS81, Bud83] and set
language SETL [Sch75]. It uses a static single-assignment(SSA) based intermediate
representation, and inlines all functions and scripts into one large function. The
Falcon project also curated a set of MATLAB benchmarks to measure the performance
of their compiler. Several of our benchmarks are originally from Falcon’s benchmark
suite.
- MCFOR is a prototype MATLAB-to-Fortran 95 generator developed by the McLAB
research group and paved way for further research (of which MIX10 is a part) into
developing efficient static MATLAB compilers for MATLAB. MC2FOR is the second
generation MATLAB-to-Fortran 95 compiler built on top of the Tamer and MCSAF
static analysis tools. MIX10 and MC2FOR share some of the solutions that extend
the Tamer tool. We have also used MC2FOR for our performance evaluation. A good
performance by both MIX10 and MC2FOR further validates the strength of our
compilation techniques.
- MAJIC (MATLAB Just-In-time Compiler) [AP02] is a continuation of the Falcon
project. It aims to exploit optimization opportunities in the following three areashttp://polaris.cs.uiuc.edu/majic/techniques.html :
(1) source-level optimizations for matrix-based operations; (2) just-in-time compilation
to defer compilation as much as possible and thus minimize the effects of challenges
raised by MATLAB’s "wild" nature as we discussed in Chapter 6; and (3) specialized
optimizations for operations on sparse matrices.
- MENHIR [CB98] is a retargetable MATLAB compiler that can generate C or Fortran
code based on a target system description(MTSD). MTSD describes target system’s
properties and implementation details and thus allows efficient code generation that
exploits optimized sequential and parallel libraries.
- MATCH [Joi03] is a library based compilation environment for distributed
heterogeneous adaptive computing systems consisting of field-programmable gate
arrays and digital signal processors. It parallelizes MATLAB code based on user
directives and generates C code that can call different runtime libraries.
- Otter [QMSZ98b] is a MATLAB to C compiler that targets parallel computers
supporting parallel numerical libraries like ScaLAPACK [CDD+95]. It would be
interesting, as a future work, to compare performance of the Otter compiler to that of
MIX10 when it supports the parallel compilation of MATLAB more effectively.
A major difference between MIX10 and these compilers is that MIX10 targets an object
oriented language with high-level array abstractions, and which is itself source-to-source
compiled, whereas all the above mentioned projects either target JIT compilation or static
compilation to either Fortran, which is itself an array based language and in fact was the precursor
of MATLAB, or C, which is a fairly low-level language with advanced native compilers. Even
though some of the techniques used by these compilers were helpful in generating X10 code for
simple MATLAB constructs, the novelty of MIX10 lies in the fact that it identified major
challenges involved in efficiently compiling MATLAB arrays and array based operations
to X10 and achieved a performance comparable to that of compilers targeting C and
Fortran.
10.3 Compilers Targeting X10
In terms of source-to-source compilers for X10, we are aware of two other projects. StreamX10 is
a stream programming framework based on X10 [WTLY12]. StreamX10 consists of a stream
programming language COStream and a compiler which translates programs in COStream to
parallel X10 code. Tetsu discusses the design of a Ruby-based DSL for parallel programming
that is compiled to X10 [Soh11]. Both these projects focus on compiling a parallel
programming language to X10, a more efficient and generic parallel programming
language. In the future, we would like to study these projects in more depth and hope to
get useful insights into efficiently using X10 as a target language for parallelism in
MATLAB.
Chapter 11
Conclusions and Future Work
___________________________________________________________________________________
11.1 Conclusions
This thesis is about providing a bridge between two communities, the scientists/engineers/students
who like to program in MATLAB on one side; and the programming language and compiler
community who have designed elegant languages and powerful compiler techniques on the other
side.
The X10 language has been designed to provide high-level array and concurrency
abstractions, and our main goal was to develop a tool that would allow programmers to
automatically convert their MATLAB code to efficient X10 code. In this way programmers can
port their existing MATLAB code to X10, or continue to develop in MATLAB and use our MIX10
compiler as a backend to generate X10 code. Since X10 is publicly available under the Eclipse
Public License (x10-lang.org/home/x10-license.html), users could have efficient
high-performance code that they could freely distribute. Further, X10 itself can compile the code
to either Java or C++, so our tool could be used in a tool chain to convert MATLAB to those
languages as well.
Our tool is part of the McLab project, which is entirely open source. Thus, we are providing
an infrastructure for other compiler researchers to build upon this work, or to use some of our
approaches to handle other popular languages such as R.
In this thesis we demonstrated the end-to-end organization of the MIX10 tool,
and we identified that the correct handling of arrays, the minimization of casting by
safely mapping MATLAB double variables to X10 integer variables via IntegerOkay
analysis, and handling concurrency features were the key challenges. We developed
a custom version of X10’s rail-backed simple arrays, and identified where and how
this could be used for generating efficient X10 code. For cases where precise static
array shape and type information is not available, we showed how we can use the very
flexible region-based arrays in X10, and our experiments demonstrated that it is very
important to use the simple rail-backed arrays, for both the Java and C++ backends for
X10.
Our experiments show that our generated X10 code is competitive with other state-of-the art
code generators which target more traditional languages like C and Fortran. The C++ X10
backend produces faster code than the Java backend, but good performance is achieved in both
cases.
One of the main motivations of choosing X10 as the target language is that it supports
high-performance computing, which is often desirable for the computation-intensive applications
developed by the engineers and scientists. To demonstrate how to take advantage of X10’s
concurrency, we presented an effective translation of the MATLAB parfor construct to
semantically equivalent X10.
Our experiments showed significant performance gains for our generated parallel
X10 code, as compared to MATLAB’s parallel toolbox. This confirms that compiling
MATLAB to a modern high-performance language can lead to significant performance
improvements.
In the process of developing MIX10, we also stressed the X10 compiler with machine
generated code and found it to be mostly robust and efficient. We found that the X10 Java
backend’s optimizations may in some cases generate Java code that is too large to be JIT
compiled. We also found the random number generation for the C++ backend to be slower than
that for the Java backend. We reported our feedback to the X10 development team and hope
that our findings would help to make X10 even better. Overall, we found that with
the right techniques, X10 can be used as an effective and efficient target language
for scientific and array-based languages, for both, the sequential core and the parallel
part.
11.2 Future Work
Based on our positive experiences to date, we plan to continue improving the MIX10 tool. There
are three major areas where we plan to take ahead the development of MIX10, with the aim of
making it more complete and more efficient:
-
Exploiting parallelism
- To help us better understand and efficiently exploit the inherent
concurrency in the MATLAB programs, first of all we would like to thoroughly
evaluate and fine tune the concurrency constructs we introduced in MATLAB via
structured comments, and parallelism of the vectorized operations. Further, we would
like to experiment to find the best way to tune the generated code for different sorts of
parallel architectures. We are also planning to further our research into the direction
of automatically parallelizing MATLAB codes through static analysis mixed with
run-time checks.
-
Efficient builtin implementation
- One of the greatest strengths of MATLAB is its large
and efficient set of builtin libraries. This thesis concentrates more on effective and
efficient compilation of MATLAB constructs than finding the most efficient X10
implementations for the builtin operations. However, our experiments showed that
there are some key library routines such as matrix multiply and transpose for which
we need to have better X10 code for. Thus, there is scope for more work on X10
libraries, which could also be useful for other source-to-source compilers targeting
X10.
-
Readability
- The code that we generate is already quite clean, but has a quite low-level
structure, which might not be easily readable for non-experienced X10 programmers.
We would like to apply further transformations on it to aggregate some low-level
expressions, and to make the generated code look as “natural" as possible. This would
help MIX10 users, who are familiar with X10, to easily fine-tune the generated
X10 code to better suite their execution environments. It would also help in easy
maintenance of the generated X10 code, and better integration with hand-written
X10 code.
Our tool is open source, and we hope that the other research teams will use our
infrastructure, as well as learn from our experiences of generating effective and efficient X10
code.
Bibliography
___________________________________________________________________________________
[AP02] George Almási and David Padua. MaJIC: compiling MATLAB for speed
and responsiveness. In PLDI ’02: Proceedings of the ACM SIGPLAN 2002
Conference on Programming language design and implementation, Berlin,
Germany, 2002, pages 294–303. ACM.
[BKSE12] Jeff Bezanson, Stefan Karpinski, Viral B. Shah, and Alan Edelman. Julia:
A Fast Dynamic Language for Technical Computing. CoRR, abs/1209.5145,
2012.
[Bud83] Timothy A. Budd. An APL compiler for the UNIX timesharing system. In
APL ’83: Proceedings of the international conference on APL, Washington,
D.C., United States, 1983, pages 205–209. ACM, New York, NY, USA.
[CB98] Stéphane Chauveau and François Bodin. Menhir: An Environment for High
Performance Matlab. In LCR ’98: Selected Papers from the 4th International
Workshop on Languages, Compilers, and Run-Time Systems for Scalable
Computers, 1998, pages 27–40. Springer-Verlag, London, UK.
[CBP+12] E Coman, M Brewster, S Popuri, A Raim, and M Gobbert. A Comparative
Evaluation of Matlab, Octave, FreeMat, Scilab, R, and IDL on Tara. Technical
report, Baltimore County, US, 2012.
[CDD+95] J. Choi, J. Demmel, I. Dhillon, J. Dongarra, S. Ostrouchov, A. Petitet,
K. Staney, D. Walker, and R. C. Whaley. LAPACK Working Note 95:
ScaLAPACK: A Portable Linear Algebra Library for Distributed Memory
Computers – Design Issues and Performance. Technical report, Knoxville,
TN, USA, 1995.
[DH12a] Jesse Doherty and Laurie Hendren. McSAF: A static analysis framework for
MATLAB. In Proceedings of ECOOP 2012, 2012, pages 132–155.
[DH12b] Anton Dubrau and Laurie Hendren. Taming MATLAB. In Proceedings of
OOPSLA 2012, 2012, pages 503–522.
[DHR11] Jesse Doherty, Laurie Hendren, and Soroush Radpour. Kind analysis for
MATLAB. In In Proceedings of OOPSLA 2011, 2011, pages 99–118.
[DKB] Eugene Ingerman Demetrios Kyriakis and Samit Basu. Freemat.
http://freemat.sourceforge.net/.
[Doh11] Jesse Doherty. McSAF: An Extensible Static Analysis Framework for the
MATLAB Language. Master’s thesis, McGill University, December 2011.
[Dub12] Anton Dubrau. Taming matlab. Master’s thesis, April 2012.
[EH04] Torbjörn Ekman and Görel Hedin. Reusable language specifications
in JastAdd II. In Thomas Cleenewerck, editor, Evolution and Reuse
of Language Specifications for DSLs (ERLS), 2004. Available from:
http://prog.vub.ac.be/~thomas/ERLS/Ekman.pdf.
[IBM12] IBM. X10 programming language. http://x10-lang.org, February
2012.
[IBM13a] IBM. APGAS programming in X10 2.4, 2013.
http://x10-lang.org/documentation/tutorials/apgas-programming-in-x10-24.html.
[IBM13b] IBM. An introduction to X10, 2013.
http://x10.sourceforge.net/documentation/intro/latest/html/node4.html.
[INR09] INRIA. Scilab, 2009. http://www.scilab.org/platform/.
[jas] JastAdd. http://jastadd.org/.
[JB01] Pramod G. Joisha and Prithviraj Banerjee. Correctly detecting intrinsic type
errors in typeless languages such as MATLAB. In APL ’01: Proceedings of
the 2001 conference on APL, New Haven, Connecticut, 2001, pages 7–21.
ACM, New York, NY, USA.
[Joi03] Pramod G. Joisha. a MATLAB-to-C translator, 2003.
 http://www.ece.northwestern.edu/cpdc/pjoisha/mat2c/
http://www.ece.northwestern.edu/cpdc/pjoisha/mat2c/ .
[LH14] Xu Li and Laurie Hendren. Mc2for: A tool for automatically translating
matlab to fortran 95. In In Proceedings of CSMR-WCRE 2014, 2014, pages
234–243.
[Li09] Jun Li. McFor: A MATLAB to FORTRAN 95 Compiler. Master’s thesis,
McGill University, August 2009.
[Mata] MathWorks. MATLAB Coder.
http://www.mathworks.com/products/matlab-coder/.
[Matb] Mathworks. Reduction variables. http://www.mathworks.com/help/distcomp/advanced-topics.html#bq_of7_-3.
[Mat13] MathWorks. Parallel computing toolbox, 2013.
http://www.mathworks.com/products/parallel-computing/.
[Mol] Cleve Moler. The Growth of MATLAB
and The MathWorks over Two Decades.
http://www.mathworks.com/company/newsletters/news_notes/clevescorner/jan06.pdf.
[Oct] GNU Octave.
http://www.gnu.org/software/octave/index.html.
[PAG11] Ashwin
Prasad, Jayvant Anantpur, and R. Govindarajan. Automatic compilation of
MATLAB programs for synergistic execution on heterogeneous processors.
In Proceedings of the 32nd ACM SIGPLAN conference on Programming
language design and implementation, San Jose, California, USA, 2011, PLDI
’11, pages 152–163. ACM, New York, NY, USA.
[QMSZ98a]Michael J. Quinn, Alexey Malishevsky, Nagajagadeswar Seelam, and Yan
Zhao. Preliminary Results from a Parallel MATLAB Compiler. In
Proceedings of Int. Parallel Processing Symp., 1998, IPPS, pages 81–87.
[QMSZ98b]Michael J. Quinn, Alexey Malishevsky, Nagajagadeswar Seelam, and Yan
Zhao. Preliminary Results from a Parallel MATLAB Compiler. In Proc. Int.
Parallel Processing Symp. (IPPS, 1998, pages 81–87. IEEE CS Press.
[RP99] Luiz De Rose and David Padua. Techniques for the translation of MATLAB
programs into Fortran 90. ACM Trans. Program. Lang. Syst., 21(2):286–323,
1999.
[SBP+12] Vijay Saraswat, Bard Bloom, Igor Peshansky, Olivier Tardieu, and David
Grove. X10 Language Specification, Version 2.2. January 2012.
[Sch75] J. T. Schwartz. Automatic data structure choice in a language of very high
level. Commun. ACM, 18(12):722–728, 1975.
[Sci] Scipy.org. Numpy. http://www.numpy.org/.
[Soh11] Tetsu Soh. Design and implementation of a DSL based on Ruby for parallel
programming. Technical report, The University of Tokyo, January 2011.
[The02] The Mathworks. Technology Backgrounder:
Accelerating MATLAB, September 2002.
http://www.mathworks.com/company/newsletters/digest/sept02/accel_matlab.pdf.
[WS81] Zvi Weiss and Harry J. Saal. Compile time syntax analysis of APL programs.
In APL ’81: Proceedings of the international conference on APL, San
Francisco, California, United States, 1981, pages 313–320. ACM, New York,
NY, USA.
[WTLY12] Haitao Wei, Hong Tan, Xiaoxian Liu, and Junqing Yu. StreamX10: a stream
programming framework on X10. In Proceedings of the 2012 ACM SIGPLAN
X10 Workshop, Beijing, China, 2012, X10 ’12, pages 1:1–1:6. ACM, New
York, NY, USA.
Appendix A
.
[LH14] Xu Li and Laurie Hendren. Mc2for: A tool for automatically translating
matlab to fortran 95. In In Proceedings of CSMR-WCRE 2014, 2014, pages
234–243.
[Li09] Jun Li. McFor: A MATLAB to FORTRAN 95 Compiler. Master’s thesis,
McGill University, August 2009.
[Mata] MathWorks. MATLAB Coder.
http://www.mathworks.com/products/matlab-coder/.
[Matb] Mathworks. Reduction variables. http://www.mathworks.com/help/distcomp/advanced-topics.html#bq_of7_-3.
[Mat13] MathWorks. Parallel computing toolbox, 2013.
http://www.mathworks.com/products/parallel-computing/.
[Mol] Cleve Moler. The Growth of MATLAB
and The MathWorks over Two Decades.
http://www.mathworks.com/company/newsletters/news_notes/clevescorner/jan06.pdf.
[Oct] GNU Octave.
http://www.gnu.org/software/octave/index.html.
[PAG11] Ashwin
Prasad, Jayvant Anantpur, and R. Govindarajan. Automatic compilation of
MATLAB programs for synergistic execution on heterogeneous processors.
In Proceedings of the 32nd ACM SIGPLAN conference on Programming
language design and implementation, San Jose, California, USA, 2011, PLDI
’11, pages 152–163. ACM, New York, NY, USA.
[QMSZ98a]Michael J. Quinn, Alexey Malishevsky, Nagajagadeswar Seelam, and Yan
Zhao. Preliminary Results from a Parallel MATLAB Compiler. In
Proceedings of Int. Parallel Processing Symp., 1998, IPPS, pages 81–87.
[QMSZ98b]Michael J. Quinn, Alexey Malishevsky, Nagajagadeswar Seelam, and Yan
Zhao. Preliminary Results from a Parallel MATLAB Compiler. In Proc. Int.
Parallel Processing Symp. (IPPS, 1998, pages 81–87. IEEE CS Press.
[RP99] Luiz De Rose and David Padua. Techniques for the translation of MATLAB
programs into Fortran 90. ACM Trans. Program. Lang. Syst., 21(2):286–323,
1999.
[SBP+12] Vijay Saraswat, Bard Bloom, Igor Peshansky, Olivier Tardieu, and David
Grove. X10 Language Specification, Version 2.2. January 2012.
[Sch75] J. T. Schwartz. Automatic data structure choice in a language of very high
level. Commun. ACM, 18(12):722–728, 1975.
[Sci] Scipy.org. Numpy. http://www.numpy.org/.
[Soh11] Tetsu Soh. Design and implementation of a DSL based on Ruby for parallel
programming. Technical report, The University of Tokyo, January 2011.
[The02] The Mathworks. Technology Backgrounder:
Accelerating MATLAB, September 2002.
http://www.mathworks.com/company/newsletters/digest/sept02/accel_matlab.pdf.
[WS81] Zvi Weiss and Harry J. Saal. Compile time syntax analysis of APL programs.
In APL ’81: Proceedings of the international conference on APL, San
Francisco, California, United States, 1981, pages 313–320. ACM, New York,
NY, USA.
[WTLY12] Haitao Wei, Hong Tan, Xiaoxian Liu, and Junqing Yu. StreamX10: a stream
programming framework on X10. In Proceedings of the 2012 ACM SIGPLAN
X10 Workshop, Beijing, China, 2012, X10 ’12, pages 1:1–1:6. ACM, New
York, NY, USA.
Appendix A
XML structure for builtin framework
___________________________________________________________________________________
The below listing gives the XML structure for the builtin operation plus. It contains two
upper level nodes for each real and complex numbers. Each of these have specialization nodes for
the simple arrays of different dimensions, and the region arrays. Each of the specializations has 5
types of implementations.
1<plus> 2 <real> 3 <simple_array> 4 <array_1> 5 <type1> 6 { 7 val x: Double; 8 x = a+b; 9 return x; 10 } 11 </type1> 12 <type2> 13 {a.rank == b.rank}{ 14 val x = new Array[Double](a.region); 15 for (p in a.indices()){ 16 x(p) = a(p)+ b(p); 17 } 18 return x; 19 } 20 </type2> 21 <type3> 22 { 23 val x = new Array[Double](b.region); 24 for (p in b.region){ 25 x(p) = a+ b(p); 26 } 27 return x; 28 } 29 </type3> 30 <type4> 31 { 32 val x = new Array[Double](a.region); 33 for (p in a.region){ 34 x(p) = a(p)+ b; 35 } 36 return x; 37 } 38 </type4> 39 <type5> 40 </type5> 41 </array_1> 42 <array_2> 43 <type1> 44 { 45 val x: Double; 46 x = a+b; 47 return x; 48 } 49 </type1> 50 <type2> 51 {a.rank == b.rank}{ 52 val x = new Array[Double](a.region); 53 for (p in a.indices()){ 54 x(p) = a(p)+ b(p); 55 } 56 return x; 57 } 58 </type2> 59 <type3> 60 { 61 val x = new Array[Double](b.region); 62 for (p in b.region){ 63 x(p) = a+ b(p); 64 } 65 return x; 66 } 67 </type3> 68 <type4> 69 { 70 val x = new Array[Double](a.region); 71 for (p in a.region){ 72 x(p) = a(p)+ b; 73 } 74 return x; 75 } 76 </type4> 77 <type5> 78 </type5> 79 </array_2> 80 <array_3> 81 <type1> 82 { 83 val x: Double; 84 x = a+b; 85 return x; 86 } 87 </type1> 88 <type2> 89 {a.rank == b.rank}{ 90 val x = new Array[Double](a.region); 91 for (p in a.indices()){ 92 x(p) = a(p)+ b(p); 93 } 94 return x; 95 } 96 </type2> 97 <type3> 98 { 99 val x = new Array[Double](b.region); 100 for (p in b.region){ 101 x(p) = a+ b(p); 102 } 103 return x; 104 } 105 </type3> 106 <type4> 107 { 108 val x = new Array[Double](a.region); 109 for (p in a.region){ 110 x(p) = a(p)+ b; 111 } 112 return x; 113 } 114 </type4> 115 <type5> 116 </type5> 117 </array_3> 118 </simple_array> 119 <region_array> 120 <type1> 121 { 122 val x: Double; 123 x = a+b; 124 return x; 125 } 126 </type1> 127 <type2> 128 {a.rank == b.rank}{ 129 val x = new Array[Double](a.region); 130 for (p in a.region){ 131 x(p) = a(p)+ b(p); 132 } 133 return x; 134 } 135 </type2> 136 <type3> 137 { 138 val x = new Array[Double](b.region); 139 for (p in b.region){ 140 x(p) = a+ b(p); 141 } 142 return x; 143 } 144 </type3> 145 <type4> 146 { 147 val x = new Array[Double](a.region); 148 for (p in a.region){ 149 x(p) = a(p)+ b; 150 } 151 return x; 152 } 153 </type4> 154 <type5> 155 </type5> 156 </region_array> 157 </real> 158 <complex> 159 <simple_array> 160 <array_1> 161 <type1> 162 { 163 val x: Double; 164 x = a+b; 165 return x; 166 } 167 </type1> 168 <type2> 169 {a.rank == b.rank}{ 170 val x = new Array[Double](a.region); 171 for (p in a.indices()){ 172 x(p) = a(p)+ b(p); 173 } 174 return x; 175 } 176 </type2> 177 <type3> 178 { 179 val x = new Array[Double](b.region); 180 for (p in b.region){ 181 x(p) = a+ b(p); 182 } 183 return x; 184 } 185 </type3> 186 <type4> 187 { 188 val x = new Array[Double](a.region); 189 for (p in a.region){ 190 x(p) = a(p)+ b; 191 } 192 return x; 193 } 194 </type4> 195 <type5> 196 </type5> 197 </array_1> 198 <array_2> 199 <type1> 200 { 201 val x: Double; 202 x = a+b; 203 return x; 204 } 205 </type1> 206 <type2> 207 {a.rank == b.rank}{ 208 val x = new Array[Double](a.region); 209 for (p in a.indices()){ 210 x(p) = a(p)+ b(p); 211 } 212 return x; 213 } 214 </type2> 215 <type3> 216 { 217 val x = new Array[Double](b.region); 218 for (p in b.region){ 219 x(p) = a+ b(p); 220 } 221 return x; 222 } 223 </type3> 224 <type4> 225 { 226 val x = new Array[Double](a.region); 227 for (p in a.region){ 228 x(p) = a(p)+ b; 229 } 230 return x; 231 } 232 </type4> 233 <type5> 234 </type5> 235 </array_2> 236 <array_3> 237 <type1> 238 { 239 val x: Double; 240 x = a+b; 241 return x; 242 } 243 </type1> 244 <type2> 245 {a.rank == b.rank}{ 246 val x = new Array[Double](a.region); 247 for (p in a.indices()){ 248 x(p) = a(p)+ b(p); 249 } 250 return x; 251 } 252 </type2> 253 <type3> 254 { 255 val x = new Array[Double](b.region); 256 for (p in b.region){ 257 x(p) = a+ b(p); 258 } 259 return x; 260 } 261 </type3> 262 <type4> 263 { 264 val x = new Array[Double](a.region); 265 for (p in a.region){ 266 x(p) = a(p)+ b; 267 } 268 return x; 269 } 270 </type4> 271 <type5> 272 </type5> 273 </array_3> 274 </simple_array> 275 <region_array> 276 <type1> 277 { 278 val x: Double; 279 x = a+b; 280 return x; 281 } 282 </type1> 283 <type2> 284 {a.rank == b.rank}{ 285 val x = new Array[Double](a.region); 286 for (p in a.region){ 287 x(p) = a(p)+ b(p); 288 } 289 return x; 290 } 291 </type2> 292 <type3> 293 { 294 val x = new Array[Double](b.region); 295 for (p in b.region){ 296 x(p) = a+ b(p); 297 } 298 return x; 299 } 300 </type3> 301 <type4> 302 { 303 val x = new Array[Double](a.region); 304 for (p in a.region){ 305 x(p) = a(p)+ b; 306 } 307 return x; 308 } 309 </type4> 310 <type5> 311 </type5> 312 </region_array> 313 </complex> 314</plus>
Appendix B
MIX10 IR Grammar
___________________________________________________________________________________
Listing below gives the JastAdd implementation of the MIX10 IR grammar.
1Program ::= ClassBlock; 2PPHelper; 3ClassBlock ::= DeclStmt:Stmt* Method* <UseNewArray:Boolean>; 4abstract Stmt; 5CommentStmt:Stmt ::= <Comment:String>; 6BreakStmt:Stmt; 7ContinueStmt:Stmt; 8DeclStmt:Stmt ::= [MultiDeclLHS] LHS:IDInfo [RHS:Exp] 9<Mutable:Boolean> <Atomic:Boolean>; 10Literally:Stmt ::= <Verbatim:String>; 11LiterallyExp:Exp ::= <Verbatim:String>; 12BlockEnd:Literally; 13PointLooper:Stmt ::= PointID:IDUse ArrayID:IDUse 14 <DimNumber:int> [Min:Exp] [Max:Exp]; 15Method ::= MethodHeader MethodBlock; 16MethodHeader ::= ReturnType:AccessVal <Name:String> 17 Args:IDInfo*; 18ReturnStmt:Stmt ::= ReturnVal:Exp*; 19Type:AccessVal ::= <Name:String>; 20MethodBlock:StmtBlock; 21AssignStmt:Stmt ::= [MultiAssignLHS] LHS:IDInfo RHS:Exp 22 <TypeCast:Boolean> <Atomic:Boolean>; 23ExpStmt:Stmt ::= Exp; 24IDUse:Exp ::= <ID:String>; 25Dims ::= [Exp]; 26IDInfo:Exp ::= Type <Name:String> <Shape:ArrayList> 27 <didShapeChange:Boolean> <isComplex:String> Value:Exp; 28MultiDeclLHS:Exp ::= IDInfo* ; 29MultiAssignLHS:Exp ::= IDInfo* ; 30abstract UnaryExp:Exp ::= Operand:Exp; 31PreIncExp:UnaryExp; 32PreDecExp:UnaryExp; 33MinusExp:UnaryExp; 34PlusExp:UnaryExp; 35NegExp:UnaryExp; 36EmptyExp:Exp; 37RegionBuilder:Exp ::= Lower:IDUse* Upper:IDUse* 38 ArrayID:IDUse; 39SimpleArrayExp:Exp ::= Values:Exp* Point* Type; 40Point:Exp ::= CoOrd:IntLiteral* ; 41ArrayAccess:AccessVal ::= ArrayID:IDUse Indices:Exp* 42 <IsColVector:Boolean>; 43ArraySetStmt:Stmt ::= LHS:IDInfo Indices:Exp* RHS:Exp; 44SubArraySetStmt:Stmt ::= LHS:IDInfo Lower:Exp* Upper:Exp* 45 RHS:Exp; 46SubArrayGetExp:Exp ::= Lower:Exp* Upper:Exp* ArrayID:IDUse; 47abstract LiteralExp:Exp; 48Literal:LiteralExp ::= <Literal:String>; 49StringLiteral:Literal; 50FPLiteral:Literal; 51DoubleLiteral:Literal; 52IntLiteral:Literal; 53BoolLiteral:Literal; 54LongLiteral:Literal; 55CharLiteral:Literal; 56abstract BinaryExp:Exp ::= LeftOp:Exp RightOp:Exp; 57abstract ArithExp:BinaryExp; 58abstract MultiplicativeExp:ArithExp; 59MulExp:MultiplicativeExp; 60DivExp:MultiplicativeExp; 61ModExp:MultiplicativeExp; 62abstract AdditiveExp:BinaryExp; 63AddExp:AdditiveExp; 64SubExp:AdditiveExp; 65IncExp:AdditiveExp; 66DecExp:AdditiveExp; 67abstract RelationalExp:BinaryExp; 68LTExp : RelationalExp ; 69GTExp : RelationalExp ; 70LEExp : RelationalExp ; 71GEExp : RelationalExp ; 72abstract EqualityExp : RelationalExp; 73EQExp : EqualityExp ; 74NEExp : EqualityExp ; 75abstract LogicalExp:BinaryExp; 76AndExp:LogicalExp; 77OrExp:LogicalExp; 78Modifiers ::= Modifier*; 79Modifier ::= <ID:String>; 80Identifier:AccessVal ::= <Name:String>; 81ForStmt:Stmt ::= <isParfor:Boolean> AssignStmt Condition:Exp 82 Stepper:AdditiveExp LoopBody Lower:IDUse Upper:IDUse 83 Incr:IDUse; 84WhileStmt:Stmt ::= Condition:Exp LoopBody; 85StmtBlock:Stmt ::= Stmt*; 86LoopBody:StmtBlock; 87IfElseStmt:Stmt ::= IfElseIf* [ElseBody]; 88IfElseIf:Stmt ::= Condition:Exp IfBody; 89IfBody:StmtBlock; 90ElseBody:StmtBlock; 91abstract Exp; 92AtStmt:Stmt ::= Place:Exp AtBlock; 93AtBlock:StmtBlock; 94AsyncStmt:Stmt ::= AsyncBlock; 95AsyncBlock:StmtBlock; 96FinishStmt:Stmt ::= FinishBlock; 97FinishBlock:StmtBlock; 98AtomicStmt:Stmt ::= AtomicBlock; 99AtomicBlock:StmtBlock; 100WhenStmt:Stmt ::= Condition:Exp WhenBlock; 101WhenBlock:StmtBlock; 102abstract AccessVal:Exp; 103abstract MethodCall:Exp; 104BuiltinMethodCall:MethodCall ::= BuiltinMethodName:MethodId 105 Argument:Exp*; 106MethodId:AccessVal ::= <Name:String>; 107UserDefMethodCall:MethodCall ::= UserDefMethodName:MethodId 108 Argument:Exp*;
 merge operator
merge operator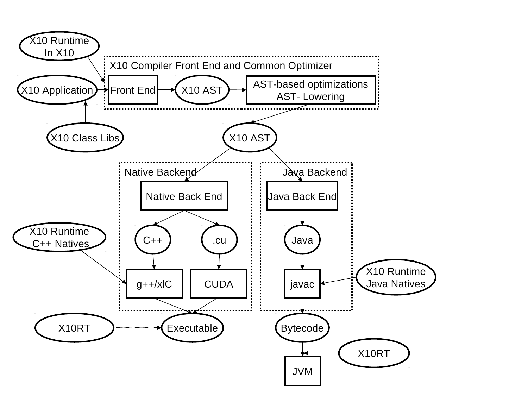


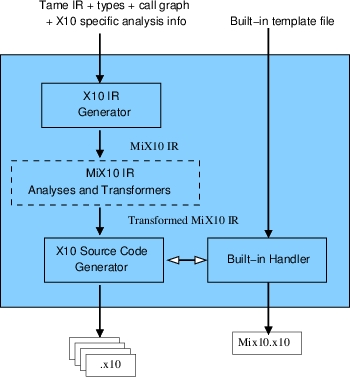













































 operator to merge the state values of various definitions and uses of a variable to obtain its
final state. Table
operator to merge the state values of various definitions and uses of a variable to obtain its
final state. Table  operator used by this analysis. In the
table,
operator used by this analysis. In the
table, 
 merge operator
merge operator
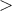 .
[LH14]
.
[LH14]